Confidence Interval for an Unknown Population Standard Deviation

🎯 Goal: Estimating a Population Mean with Unknown Standard Deviation

When we don’t know the population standard deviation (\( \sigma \)), we rely on the sample standard deviation (\( s \)) instead.

In such cases, we use the t-distribution, not the Z-distribution.

---

☕ Real-World Case: Coffee Consumption Among Remote Workers

Imagine you’re studying how much coffee remote developers drink daily. You gather data from a random sample of 25 developers and calculate:

• Sample Mean: \( \bar{x} = 3.8 \) cups/day
• Sample Standard Deviation: \( s = 1.1 \) cups
• Sample Size: \( n = 25 \)
• Confidence Level: 95% (t-critical value for \( df = 24 \) is \( t_{0.025} \approx 2.064 \))

---

📊 Step-by-Step: Building the Confidence Interval (T-Distribution)

🔹 Step 1: Calculate the Standard Error

\[ SE = \frac{s}{\sqrt{n}} = \frac{1.1}{\sqrt{25}} = 0.22 \]

---

🔹 Step 2: Find the Margin of Error

\[ ME = t \times SE = 2.064 \times 0.22 \approx 0.454 \]

---

🔹 Step 3: Construct the Confidence Interval

\[ \bar{x} \pm ME = 3.8 \pm 0.454 \]

• Lower Bound: \( 3.8 - 0.454 = 3.35 \)
• Upper Bound: \( 3.8 + 0.454 = 4.25 \)

✅ Conclusion: We are 95% confident that average coffee consumption among remote developers is between 3.35 and 4.25 cups/day.

---

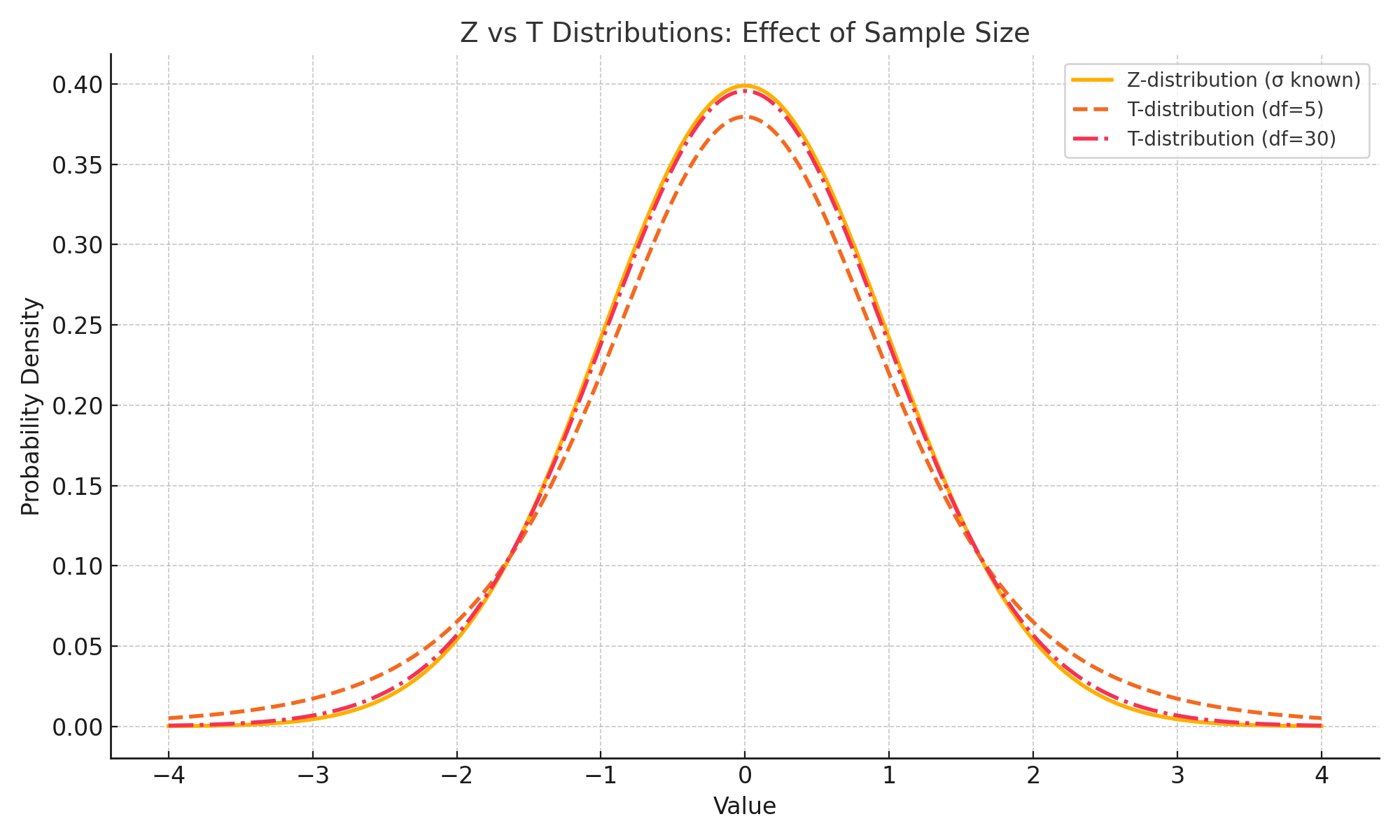
🧠 Visual Insight: Why Use the T-Distribution?

When sample sizes are small, the T-distribution is wider than the Z-distribution — reflecting greater uncertainty.
As sample size increases (and degrees of freedom rise), the T-distribution converges toward the Z-distribution.
This is why we use T when σ is unknown and rely on sample SD.

---

🧠 Level Up: Why This Matters for Machine Learning

In ML, your data is often a sample from a larger unknown population.

• ⚖️ When model performance varies across subgroups, you need confidence intervals to quantify uncertainty.
• 🧪 In A/B testing or model benchmarking, if the standard deviation is unknown, the T-distribution helps you generalize correctly from sample data.

📈 Understanding this concept sharpens your ability to evaluate models statistically — especially in cases where your dataset is small or imbalanced.

---

🧠 Why These Formulas Work: Intuition Behind SE and T

The formula for standard error:

[ \(SE = \frac{s}{\sqrt{n}}\) ]

tells us how much the sample mean is expected to vary from one random sample to another.

• Dividing by \( \sqrt{n} \) reflects the idea that larger samples are more stable.
• As \( n \) increases, your sample mean gets closer to the true mean — which shrinks the SE and narrows the confidence interval.

The t-critical value accounts for extra uncertainty when we don’t know the population standard deviation (\( \sigma \)).

• With small samples (low degrees of freedom), the T-distribution is wider than the Z-distribution.
• That’s why the margin of error is larger — it’s protecting you from overconfidence when data is scarce.

🧠 In essence, this math adjusts for the fact that your estimate is shakier when you have less data or less certainty.

---

🐍 Python in Practice: CI with Unknown Standard Deviation (T-Distribution)

import numpy as np
import scipy.stats as stats

# Given
sample_mean = 3.8
sample_std = 1.1
n = 25
df = n - 1
t_critical = stats.t.ppf(1 - 0.025, df)

# Standard Error
se = sample_std / np.sqrt(n)

# Margin of Error
me = t_critical * se

# Confidence Interval
ci_lower = sample_mean - me
ci_upper = sample_mean + me

print(f"95% CI: ({ci_lower:.2f}, {ci_upper:.2f})")

📏 Quick Reference: Steps to Calculate

Component	Formula	Value
Sample Mean (\( \bar{x} \))	—	3.8 cups
Sample SD (\( s \))	—	1.1 cups
Sample Size (\( n \))	—	25
Degrees of Freedom	\( n - 1 \)	24
t-critical (95%)	\( t_{0.025,24} \approx 2.064 \)	—
Standard Error	\( \frac{s}{\sqrt{n}} \)	0.22
Margin of Error	\( t \times SE \)	0.454
CI	\( \bar{x} \pm ME \)	(3.35, 4.25)

---

✅ Best Practices for T-Based Confidence Intervals

• 📚 Always use the T-distribution when \[ (\sigma) \] is unknown
• 📈 Report degrees of freedom (n − 1) for transparency
• 👥 Use sufficiently large samples (n > 30) to better approximate normality
• 📉 Check data symmetry — the T-distribution assumes the sample is roughly normal
• 🧾 Always report both the point estimate and the confidence interval range

---

⚠ Common Pitfalls

• 🚫 Using the Z-distribution when σ is unknown
• 🔁 Forgetting degrees of freedom when looking up critical t-values
• 😬 Assuming small samples are normally distributed without checking
• 📉 Ignoring skewness or outliers — the T-distribution is sensitive when n is small
• 🤔 Confusing confidence intervals with probability — CI reflects method reliability, not certainty about a single estimate

---

🧠 Level Up: When to Switch from T to Z

• Use the Z-distribution when:
  • Population standard deviation (σ) is known
  • Sample size is large (n > 30) and the Central Limit Theorem applies
• Use the T-distribution when:
  • σ is unknown and estimated using the sample standard deviation
  • You are working with small samples (n < 30)

In practice: You will almost always use the T-distribution — Z is a special theoretical case.

📌 Try It Yourself: T-Interval Confidence Quiz

Q1: When should you use the T-distribution instead of Z?

💡 Show Answer

When the population standard deviation is **unknown**.

Q2: What’s the standard error formula when using sample SD?

💡 Show Answer

\[ ( SE = \\frac{s}{\\sqrt{n}} \\) \]

Q3: Why is “degrees of freedom” used in the t-distribution?

💡 Show Answer

Because we estimate the variance from the sample, so we lose 1 degree of freedom.

Q4: Does increasing the sample size reduce the margin of error?

💡 Show Answer

Yes — increasing \[ ( n ) \] reduces SE, which tightens the confidence interval.

---

🔜 What’s Next?

In the next post, we’ll explore how to compare two population means using two-sample T-tests — crucial for A/B testing and hypothesis evaluation in machine learning.

---

💬 Got a Question?

Leave a comment or open an issue on GitHub — I love connecting with other learners and builders. 🔁