Confidence Intervals: A Full Case Study on Mean vs Proportion

🎓 Two Case Studies: Estimating Means and Proportions in Data Science Student

In this comprehensive example, you’ll learn how to calculate confidence intervals for two different goals:

• Estimating a population average (mean) using the T-distribution
• Estimating a population proportion using the Z-distribution

---

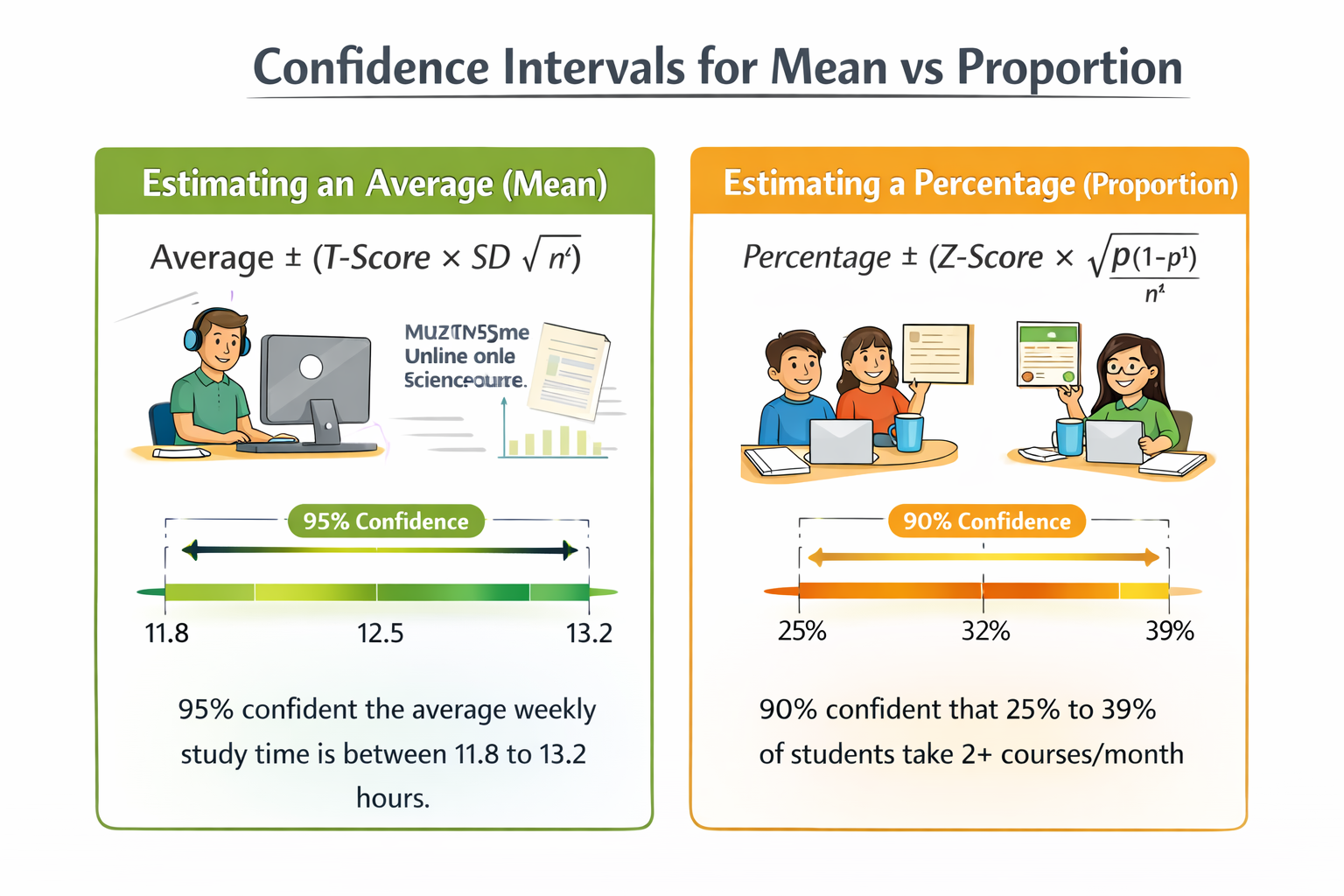
📌 Scenario A: Estimating an Average (Mean)

🎯 Goal:

Estimate the average number of hours Data Science students spend watching online courses weekly.

📊 Data:

• Sample Size (\( n \)) = 120 students
• Sample Mean (\( \bar{x} \)) = 12.5 hours
• Sample Standard Deviation (\( S \)) = 4.2 hours
• Confidence Level = 95%

🧮 Step-by-Step:

1. Use T-Distribution (since we’re estimating a mean and \( \sigma \) is unknown)

2. Degrees of Freedom: \[ df = n - 1 = 119 \]

3. T-score for 95% confidence and df = 100 (close to 119):
\[ t = 1.984 \]

4. Margin of Error (ME): \[ ME = 1.984 \times \frac{4.2}{\sqrt{120}} \approx 0.76 \]

5. Confidence Interval: \[ 12.5 \pm 0.76 \Rightarrow [11.74, 13.26] \]

✅ Conclusion: We are 95% confident that the average number of hours Data Science students spend on online learning weekly is between 11.74 and 13.26 hours.

---

📌 Scenario B: Estimating a Proportion

🎯 Goal:

Estimate the percentage of Data Science students who complete more than one course per month.

📊 Data:

• Sample Size (\( n \)) = 120 students
• Sample Proportion (\( \hat{p} \)) = 0.32 (32%)
• Confidence Level = 90%

🧮 Step-by-Step:

1. Use Z-Distribution (proportions always use Z)

2. Z-score for 90% confidence: \[ z = 1.645 \]

3. Standard Error (SE): \[ SE = \sqrt{\frac{0.32 \cdot 0.68}{120}} \approx 0.043 \]

4. Margin of Error (ME): \[ ME = 1.645 \times 0.043 \approx 0.071 \]

5. Confidence Interval: \[ 0.32 \pm 0.071 \Rightarrow [0.249, 0.391] \]

✅ Conclusion: We are 90% confident that between 24.9% and 39.1% of Data Science students complete more than one course per month.

---

---

🧭 Practical Plan: Choosing the Right Method

Follow this plan anytime you have data and want to estimate population parameters confidently.

---

✅ Step 1: Define Your Objective

Type of Measurement	Go To Step
Average (Mean)	Step 2A
Percentage	Step 2B

---

📏 Step 2A: Estimating a Mean

Use the formula:

\[ \text{Mean} \pm \left( \text{T-Score} \times \frac{S}{\sqrt{n}} \right) \]

• Use \( df = n - 1 \) to get your T-score
• Works best when \( \sigma \) is unknown (almost always in real-world data)

---

📊 Step 2B: Estimating a Proportion

Use the formula:

\[ \text{Proportion} \pm \left( Z \times \sqrt{\frac{p(1-p)}{n}} \right) \]

• Use Z-scores for your confidence level:
  • 90% → 1.645
  • 95% → 1.96
  • 99% → 2.58

---

🧾 Step 3: Communicate the Results

“We are [Confidence Level]% confident that the true [average/percentage] lies between [lower bound] and [upper bound], based on a sample of [n] participants.”

---

✅ Best Practices for Confidence Intervals

• 🎯 Use the T-distribution when estimating means with unknown population standard deviation (which is almost always the case)
• 📐 Use the Z-distribution for proportions since it relies on known sample proportions and large enough n
• 🧪 Ensure sample size is large enough: at least 30 for means, and both np and n(1-p) ≥ 15 for proportions
• 📈 Always report both the point estimate and the confidence interval for clarity
• 🔍 State your confidence level clearly in conclusions: “We are 95% confident that…”

---

⚠ Common Pitfalls

• 🚫 Using Z-distribution for means when population standard deviation is unknown
• 😵‍💫 Misinterpreting confidence intervals — it’s about method reliability, not a specific probability
• 📉 Failing to check assumptions (normality for small n, np ≥ 15 rule for proportions)
• 📉 Using too small a sample size leading to wide, less useful intervals
• 🤷 Reporting CI without context (e.g., sample size, confidence level, or what’s being measured)

---

🧠 Level-Up: Choosing Between T and Z

• Use T-distribution when:
  • Estimating a mean
  • Population standard deviation (σ) is unknown
  • Sample size is small (n < 30)
• Use Z-distribution when:
  • Estimating a proportion (e.g., % of users who clicked)
  • Sample size is large

Tip: T is used far more often than Z in real-world analysis involving averages.

---

🧬 Why It Matters in Machine Learning

• 📊 Model Evaluation: Confidence intervals help quantify uncertainty in accuracy, precision, recall, etc.
• 📉 Generalization: CI offers a way to express how your model might perform on unseen data
• 🤖 A/B Testing: CI around click-through rates or conversion proportions guide data-driven product decisions
• ⚖️ Bias Detection: Confidence intervals allow comparison across subgroups (e.g., fairness across genders or regions)

---

📌 Try It Yourself: Confidence Interval Quiz

Q1: When should you use the T-distribution?

💡 Show Answer

When estimating a mean and the population standard deviation is unknown.

Q2: What’s the formula for confidence intervals for proportions?

💡 Show Answer

\[ \hat{p} \pm Z \cdot \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}} \]

Q3: What happens when you increase your confidence level from 95% to 99%?

💡 Show Answer

The margin of error increases — your interval becomes wider.

Q4: What’s the difference between T and Z distributions?

💡 Show Answer

T-distribution is used for small samples and unknown σ, Z is used for large samples and proportions.

---

🧾 Summary: Key Takeaways

• ✅ Use T-distribution when estimating a mean with unknown population standard deviation.
• ✅ Use Z-distribution when estimating a proportion or when σ is known and sample size is large.
• 🧪 Check sample size: use T only if your sample is reasonably large or data is approximately normal.
• 🎯 Interpret CIs correctly: a 95% confidence interval means the method captures the true value 95% of the time.
• 🔍 Always report the confidence level, the estimate, and the full interval.
• 📊 Real-world data (like study hours or course completion rates) can be analyzed with these tools.
• 🤖 In ML, confidence intervals support robust reporting for metrics, A/B testing, and generalization checks.

📘 Use this post as a practical guide every time you work with statistical estimates in your analysis or models.

---

📺 Explore the Channel

🎥 Hoda Osama AI

Learn statistics and machine learning concepts step by step with visuals and real examples.

---

💬 Got a Question?

Leave a comment or open an issue on GitHub — I love connecting with other learners and builders. 🔁