Statistical Hypotheses: How to Form and Test Assumptions with Data

📊 Statistical Hypotheses: The Foundation of Significance Testing

This post introduces Statistical Hypotheses, the starting point for Significance Testing in inferential statistics. You’ll learn how to:

• Formulate null and alternative hypotheses.
• Understand the logic behind testing them.
• Apply real-world examples from tech and data scenarios.

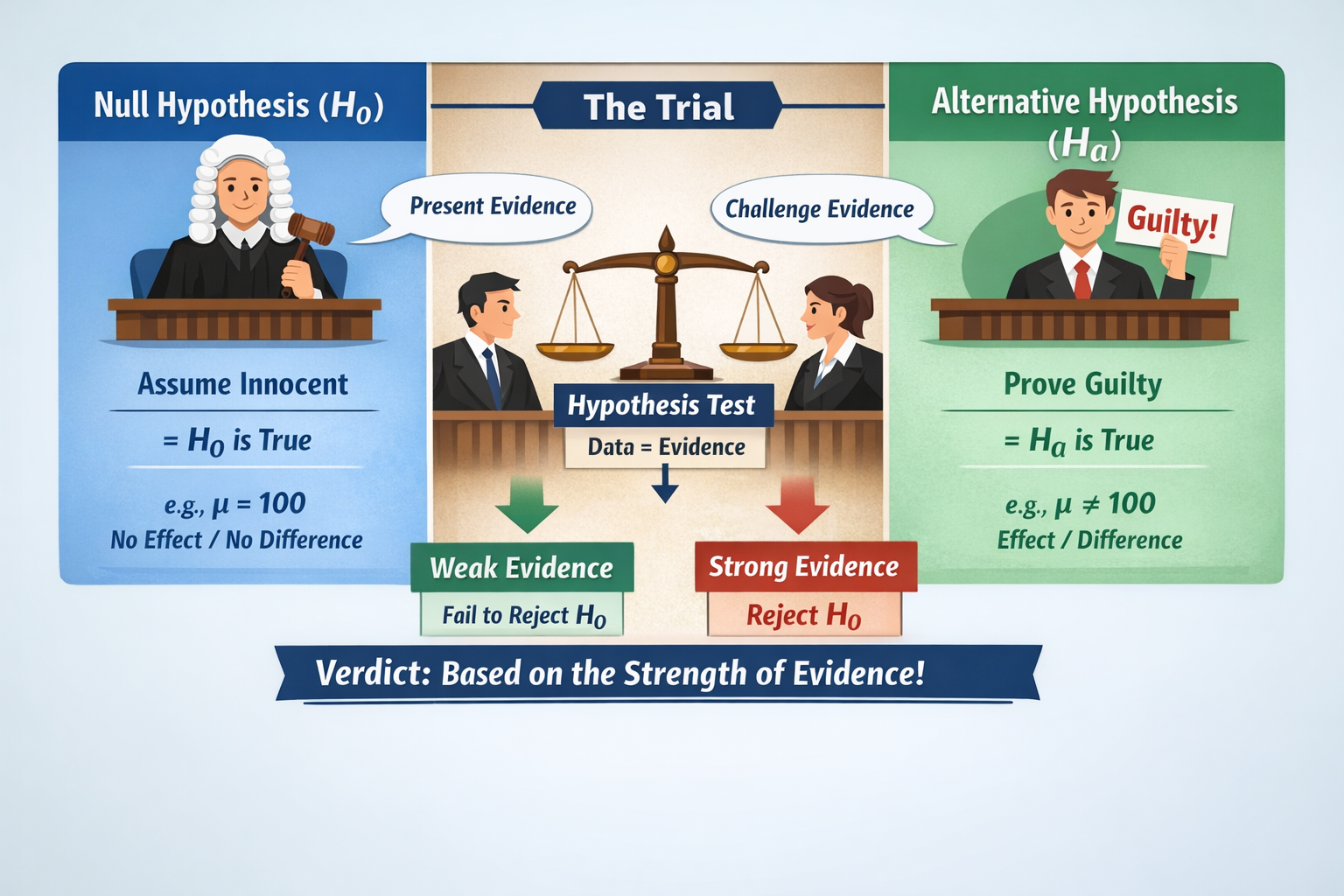
The courtroom analogy makes it clear: we assume innocence (the null hypothesis $H_0$) until evidence supports a different claim (the alternative hypothesis $H_a$).

---

🔍 Main Concepts

What is a Hypothesis?

A statistical hypothesis is a claim or assumption about a population parameter — typically a mean (μ) or proportion (p).

Types of Hypotheses:

• Null Hypothesis ($H_0$): The default assumption. States that there is no effect or no difference (e.g., $p = 0.25$).
• Alternative Hypothesis ($H_a$): What you’re trying to support — that there is an effect or difference (e.g., $p > 0.25$).
• They are mutually exclusive: only one can be true.

---

⚖️ The Courtroom Analogy

• $H_0$ = Innocent until proven guilty.
• Data = Evidence. The trial tests whether evidence strongly contradicts $H_0$.
• If the evidence is weak: we fail to reject $H_0$.
• If the evidence is strong: we reject $H_0$ in favor of $H_a$.

---

---

🧪 Real-World Examples (Updated)

📈 Example 1: Click-Through Rate (Proportion)

Scenario:
A data analyst wants to test whether the new homepage design increases click-through rates above the current benchmark of 25%.

• Null Hypothesis ($H_0$): $p = 0.25$
• Alternative Hypothesis ($H_a$): $p > 0.25$
• Type: One-tailed proportion test

If a random sample of 200 users shows that 64 clicked (click rate = 0.32), this test can determine if the difference is statistically significant or due to chance.

---

🧠 Example 2: Server Response Time (Mean)

Scenario:
An ML engineer suspects that a new backend model slows response time compared to the current standard of 120ms.

• Null Hypothesis ($H_0$): $\mu = 120$
• Alternative Hypothesis ($H_a$): $\mu > 120$
• Type: One-tailed mean test

A sample of 40 responses from the new model shows a mean of 127.5ms with a standard deviation of 15ms. Is this increase significant?

---

✅ Practical Plan: How to Formulate a Hypothesis Test

🔹 Phase 1: Define Your Claim

• Identify the Parameter: Are you testing a mean (μ) or a proportion (p)?
• Define $H_a$: What outcome do you want to support? Use inequalities ($<, >, eq$).

🔹 Phase 2: Set the Baseline

• Define $H_0$: This is the claim of “no change”, always using equality.

🔹 Phase 3: Conduct the Test

• Collect sample data.
• Analyze: Does the evidence contradict $H_0$ strongly enough?
• Conclude: Reject $H_0$ only if results are statistically significant.

⚠️ Important: If results are not significant, you do not confirm $H_0$ is true — you only “fail to reject” it due to insufficient evidence.

---

✅ Best Practices for Hypothesis Testing

• 📚 Always define both $H_0$ and $H_a$ clearly before collecting data
• 🎯 Use one-tailed tests only when your research question has a clear direction (e.g., $H_a$: $p > 0.3$)
• 📊 Select the appropriate test: Use Z-tests for proportions and T-tests for means with unknown σ
• 📈 Report the p-value and compare it with a significance level (usually 0.05)
• 🧪 Include context for your conclusion: explain practical implications of rejecting or not rejecting $H_0$

---

⚠ Common Pitfalls in Hypothesis Testing

• 🚫 Failing to define hypotheses properly before analyzing the data
• ❌ Using a one-tailed test when a two-tailed test is required
• 😬 Misinterpreting "fail to reject $H_0$" as proof that $H_0$ is true
• 🔍 Ignoring assumptions such as sample independence or normality (for T-tests)
• 📉 Basing conclusions on anecdotal or biased samples

---

🧠 Level-Up: One-Tailed vs. Two-Tailed Tests

• One-Tailed Test: Use when your alternative hypothesis points in a specific direction:
  • e.g., $H_a$: $\mu > 100$ or $p < 0.3$
• Two-Tailed Test: Use when you're testing for any difference (no specific direction):
  • e.g., $H_a$: $\mu eq 100$

Tip: When in doubt, choose the two-tailed test — it's more conservative and widely used in scientific research.

---

🧬 Why It Matters to Machine Learning

• 🤖 Model Validation: Hypothesis testing helps verify if performance improvements are statistically significant
• 🧪 A/B Testing: Common in ML product pipelines for comparing models, interfaces, or features
• 🧠 Bias Detection: You can test if certain metrics differ across subgroups (e.g., fairness audits)
• 📊 Statistical significance provides evidence that generalizes beyond training data
• ⚙️ Noise Filtering: Helps avoid overreacting to random performance fluctuations

---

📌 Try It Yourself: Hypothesis Testing Quiz

Q1: What is the null hypothesis in a significance test?

💡 Show Answer

The default assumption that there's no effect or no difference in the population.

Q2: Which hypothesis do we try to find evidence for?

💡 Show Answer

The alternative hypothesis ($H_a$).

Q3: If you fail to reject the null hypothesis, what does it mean?

💡 Show Answer

There wasn't enough evidence to support the alternative; we keep $H_0$.

Q4: When do you use a T-test instead of a Z-test?

💡 Show Answer

When the population standard deviation is unknown and you're testing a mean.

Q5: What does “statistically significant” mean in hypothesis testing?

💡 Show Answer

The result is unlikely to have occurred by random chance alone under the null hypothesis.

---

📝 Final Summary

• Hypothesis testing is a fundamental part of inferential statistics.
• It starts with a null hypothesis ($H_0$) that represents the status quo.
• You test sample data to determine whether there’s enough evidence to reject $H_0$ in favor of an alternative hypothesis ($H_a$).
• Always define your hypotheses before collecting data and use the correct test depending on whether you’re analyzing means (T-test) or proportions (Z-test).
• In machine learning, hypothesis testing helps validate models, ensure robustness, and support decision-making based on evidence rather than assumptions.

Use these principles to strengthen the credibility of your data insights. 🚀

---

📺 Explore the Channel

🎥 Hoda Osama AI

Learn statistics and machine learning concepts step by step with visuals and real examples.

---

💬 Got a Question?

Leave a comment or open an issue on GitHub — I love connecting with other learners and builders. 🔁