Correlation Between Variables: Contingency Tables and Scatter Plots

Understanding how two variables relate is a core step in data analysis — and that’s where correlation comes in.

But choosing the right correlation method depends on your data type: are your variables categorical or quantitative? In this post, we’ll break down the key approaches — from contingency tables to scatter plots — so you can analyze relationships with confidence.

---

📚 This post is part of the "Intro to Statistics" series

🔙 Previously: A Real-World Statistics Example

🔜 Next: Understanding Pearson's R

---

🎓 Real-Life Case: Study Habits and Exam Performance

Imagine a high school counselor wants to investigate the relationship between how often students study and whether they pass or fail a weekly quiz.

She surveys 30 students and records two things:

• 📚 Study Time Category: Rarely, Sometimes, Often
• ✅ Quiz Result: Pass or Fail

---

🧮 Step 1: The Contingency Table

This type of table is used for categorical variables. It shows how often combinations of categories occur.

Study Frequency \ Quiz Result	Pass	Fail	Total
Rarely	3	7	10
Sometimes	6	4	10
Often	9	1	10
Total	18	12	30

---

🔁 Step 2: Conditional Proportions

The raw counts don’t tell the full story. So we calculate the percentage of each outcome within each group.

For example:

• Among students who study Rarely, 3/10 passed = 30%
• Among those who study Often, 9/10 passed = 90%

Study Frequency	% Passed	% Failed
Rarely	30%	70%
Sometimes	60%	40%
Often	90%	10%

✅ These are conditional proportions — percentages within each row.

---

📊 Step 3: Understanding Proportions — Quick Summary

We use conditional proportions to look within groups, and marginal proportions to summarize a variable on its own.

• Conditional example:
  Among those who study Rarely → 3/10 passed = 30%
• Marginal example:
  Overall pass rate → 18/30 = 60%

📚 Want a full breakdown with examples, visual tables, and when to use each?
👉 Read: Conditional vs. Marginal Proportions →

---

🔍 Step 4: Interpreting the Categorical Correlation

The more a student studies, the more likely they are to pass.
We can see a positive association in the conditional proportions:

• Rarely study → low pass rate
• Often study → high pass rate

➡️ But contingency tables don’t quantify correlation — they only show patterns.

---

🔄 Step 5: Let’s Make It Quantitative

Now let’s change the scenario:

The counselor asks students for their exact number of study hours per week and records their quiz scores out of 100.

Here’s a sample:

Hours Studied	Quiz Score
2	50
3	55
5	65
7	70
8	76
10	85
12	92

---

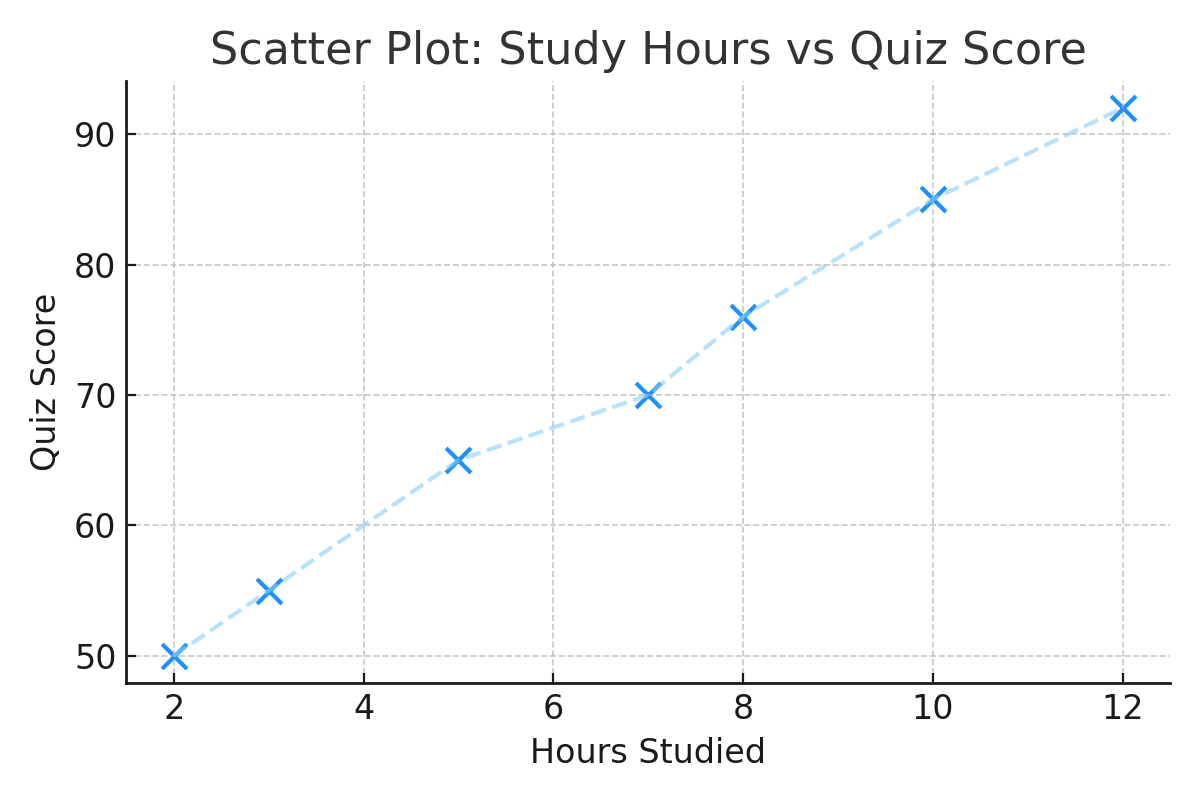
📈 Step 6: Scatter Plot

This type of plot is perfect for quantitative variables.
It helps us visually assess correlation:

• Each point = one student
• X-axis: Hours studied
• Y-axis: Quiz score

You’ll notice: the more hours students study, the higher their scores.
This is a strong positive relationship.

---

✅ Best Practices When Exploring Variable Relationships

• Start with simple visuals like scatter plots or tables before jumping into modeling.
• Use scatter plots to spot linear or curved patterns between numeric variables.
• For categorical data, contingency tables show how categories relate.
• Always ask: “Can this help my model make better predictions?”
• Use a correlation metric (like Pearson’s r) for numerical comparisons.

---

⚠ Common Pitfalls to Avoid

• Assuming correlation means causation — just because two variables move together doesn’t mean one causes the other.
• Ignoring outliers — one extreme value can distort your scatter plot or correlation result.
• Overlooking non-linear patterns — not all relationships are straight lines. Try other visuals or transformations.
• Using the wrong chart — don’t use a scatter plot for categorical data; use a contingency table instead.
• Forgetting to check variable types — always know what kind of data you're working with before analyzing relationships.

---

🧠 Level Up: Choosing the Right Correlation Approach Based on Data Types

Correlation analysis isn’t one-size-fits-all — the type of variables determines the best method:

• 📊 For two quantitative variables, measures like Pearson's r capture linear relationships.
• 📋 For two categorical variables, contingency tables and tests like Chi-square help assess association.
• 🔄 For mixed variable types, specialized methods like point-biserial correlation or ANOVA are used.

Understanding your data types ensures you pick the most powerful and appropriate analysis technique.

---

📌 Try It Yourself

Q: Imagine you're analyzing students’ test scores, and a few unusually high scores raise the mean. Which measure of center gives a more accurate picture of the typical student’s performance — mean or median?

💡 Show Answer

✅ Median — because it's resistant to outliers, unlike the mean which gets skewed. The median focuses on the middle value, so a few extreme values won't distort it, making it more reliable in such cases.

---

🤖 Why It Matters in Machine Learning

In machine learning, understanding relationships between variables helps you:

• 📊 Choose the right features for your model (feature selection).
• 📉 Detect multicollinearity — too much correlation between features can hurt model accuracy.
• 🧪 Engineer new features based on strong associations (e.g., combining study time and pass rate).
• 📈 Pick the right models — strong linear correlation? Consider regression. Categorical outcomes? Try classification.

Learning how to interpret contingency tables and scatter plots builds your EDA skills, a core part of every data science pipeline.

---

✅ Conclusion

Type of Data	Tool to Use	Example
Categorical (Nominal/Ordinal)	Contingency Table	Study Frequency vs Pass/Fail
Quantitative	Scatter Plot	Hours Studied vs Quiz Score

🧠 Choose the right tool based on your variable types.

---

💬 Got a question or suggestion?

Leave a comment below — I’d love to hear your thoughts or help if something was unclear.

---

🔜 Up Next

Next, we’ll calculate the Pearson correlation coefficient (r) — a number that tells us how strong a linear relationship really is.