Bringing It All Together: A Real-World Stats Example

In this post, we’ll walk through a real-world case study that uses core statistical tools: mean, median, standard deviation, box plots, and z-scores. Whether you’re prepping data for machine learning or analyzing student scores, these skills are essential for interpreting numbers with confidence.

---

🎓 Real-Life Scenario

Imagine you’re a school data analyst. A math teacher gives you the scores from a recent algebra quiz taken by 10 high school students.

The teacher wants to know:

• Are these scores typical?
• Are there any unusually high or low performers?
• What is the best way to summarize this small dataset?

---

📚 This post is part of the "Intro to Statistics" series

🔙 Previously: Z-Score: Comparing Values Across Distributions

🔜 Next: Correlation Between Variables

---

🧾 The Data

The scores (out of 100):

[ [44, 47, 49, 51, 52, 53, 55, 57, 90, 95] ]

---

🔍 Step 1: Type of Variable

These are quantitative values — actual test scores.
Since there are only 10 observations, we can visualize them easily.

---

📊 Step 2: Dot Plot

Here’s what the scores look like when placed on a dot plot:

Two students (scoring 90 and 95) seem to have performed far better than the rest — possible outliers.

---

📈 Step 3: Measuring the Center

To summarize where most students scored:

• Mode: None (all values are unique)
• Median: Middle two scores = ( (52 + 53) / 2 = 52.5 )
• Mean:
  \[ \bar{x} = \frac{\sum x}{n} = \frac{593}{10} = 59.3 \]

🔍 Because two students scored much higher than the rest, the mean is pulled upward, and the median gives a more typical score.

---

📐 Step 4: How Spread Out Are the Scores?

Let’s measure variability to see if most students were close to the average.

• Range = 95 − 44 = 51
• IQR:
  • Q1 = 49, Q3 = 57 → IQR = 8
• Standard Deviation (rounded):
  \[ \sigma \approx 17.0 \]

➡️ This tells us there’s a wide spread, especially due to the top scorers.

---

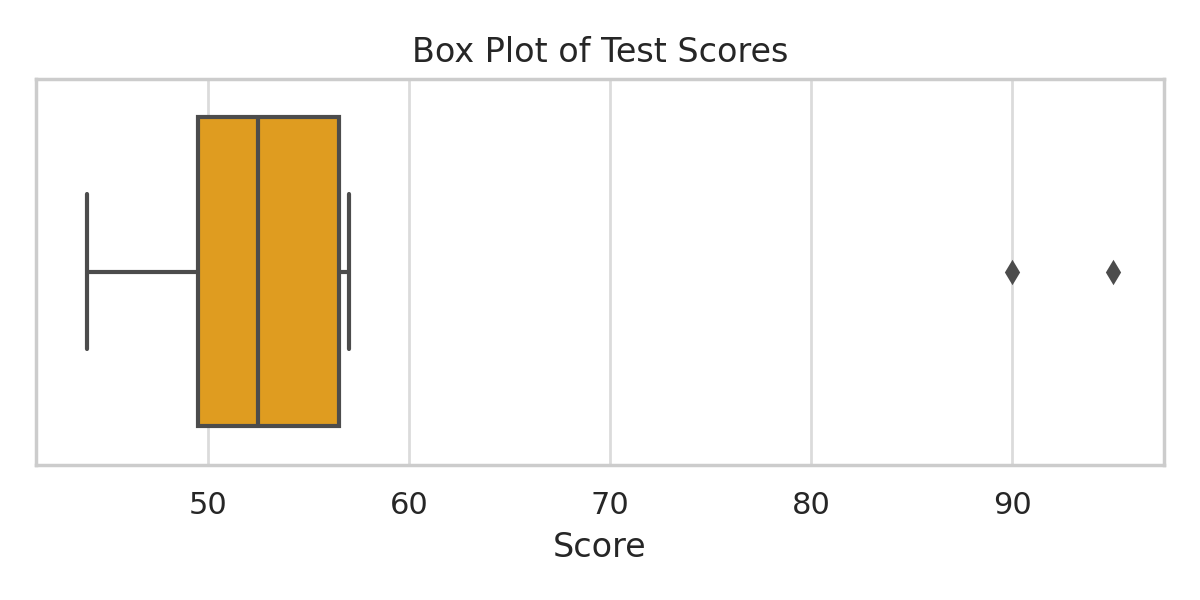
📦 Step 5: Visualizing Spread with a Box Plot

Box plots are great when you want to see:

• Center
• Spread
• Outliers — all at once

Here’s what it looks like for these scores:

You can clearly see the outliers to the far right.

---

🧮 Step 6: Z-Score for the Top Student

Let’s calculate how far the score of 90 is from the average:

\[ z = \frac{90 - 59.3}{17.0} \approx 1.8 \]

🟢 A z-score of 1.8 means this student scored 1.8 standard deviations above the mean — a strong performance.

---

🧪 Try It in Python

Here’s how to compute some of the same stats using Python:

import numpy as np

scores = [44, 47, 49, 51, 52, 53, 55, 57, 90, 95]

mean = np.mean(scores)
median = np.median(scores)
std_dev = np.std(scores)
z_score = (90 - mean) / std_dev

print("Mean:", mean)
print("Median:", median)
print("Std Dev:", std_dev)
print("Z-score for 90:", z_score)

🧠 Tip: Use ddof=1 if you’re calculating sample standard deviation.

---

📌 Try It Yourself

Q: Imagine you're analyzing students’ test scores, and a few unusually high scores raise the mean. Which measure of center gives a more accurate picture of the typical student’s performance — mean or median?

💡 Show Answer

✅ Median — because it's resistant to outliers, unlike the mean which gets skewed. The median focuses on the middle value, so a few extreme values won't distort it, making it more reliable in such cases.

---

🧠 Level Up: Interpreting Outliers and Variability in Real Data

This example highlights important concepts in real-world data analysis:

• 📉 Outliers can dramatically affect the mean but have less influence on the median and IQR.
• 📦 Box plots visually summarize both center and spread, making it easy to spot unusual values.
• 🧮 Z-scores quantify how far points deviate from the mean, helping identify exceptional cases objectively.
• 🔎 Combining these tools provides a holistic understanding of data distribution, crucial for accurate analysis and decision making.

Mastering these interpretations will improve your data intuition and prepare you for advanced statistical techniques.

---

🧠 Summary Interpretation

The teacher’s intuition was right:
Most students scored between 44–57, but two students (90, 95) scored exceptionally high, pulling the mean up.

The median and IQR give a better picture of the typical student’s performance, while the box plot and z-scores confirm the presence and magnitude of outliers.

---

💬 Have a question, feedback, or a similar example from your own data?
Feel free to share it in the comment section below — I’d love to hear your thoughts or help if something’s unclear!

---

✅ Up Next

Next time, we’ll begin our journey into probability — the language of uncertainty and how it powers statistical thinking.

Stay tuned!