Sampling Distribution of the Sample Proportion

🎯 The Sampling Distribution of the Sample Proportion

In a population, the proportion is the number of successful outcomes over the total number of cases. This proportion is denoted by \( \beta \).

For a sample, the proportion is represented by \( p \), which is an estimate of \( \beta \) (population proportion). As the sample size increases, \( p \) gets closer to \( \beta \).

• Number of samples = \( N \)
• Sample proportion = \( p \)

---

📚 This post is part of the "Intro to Statistics" series

🔙 Previously: Population, Sample, and Sampling Distributions Explained

---

🔍 Example: Proportion of Voters Supporting a Candidate

Imagine you’re conducting a poll to determine the proportion of voters supporting a political candidate in a city. Out of a sample of 1000 people:

• 600 people say they support the candidate, so the sample proportion \( p = \frac{600}{1000} = 0.6 \).

If you repeat this polling process many times, the sample proportions will vary. The more samples you take, the closer \( p \) will get to the\( \beta ), which is the true support rate in the city.

---

📊 Key Properties of the Sampling Distribution of the Sample Proportion

• As the number of samples approaches infinity, the sample proportion \( p \) will approximate the population proportion \( \beta \).
• The mean of the sampling distribution of the sample proportion is \( \mu_p = \mu \) (the population proportion).
• The sampling distribution is approximately normal if:
  • \( n \times \beta \geq 15 \)
  • \( n \times (1 - \beta) \geq 15 \)

This is because we are working with binary categorical data, where the outcomes are either “success” or “failure.”

---

🔎 Conditions for Normality

• The sampling distribution of the sample proportion will be approximately bell-shaped if:
  • \( n \times \beta \geq 15 \)
  • \( n \times (1 - \beta) \geq 15 \)

Where:

• \( n \) = sample size
• \( \beta \) = population proportion (success rate)

This ensures that the data behaves like a normal distribution and we can use standard statistical tools like Z-scores.

---

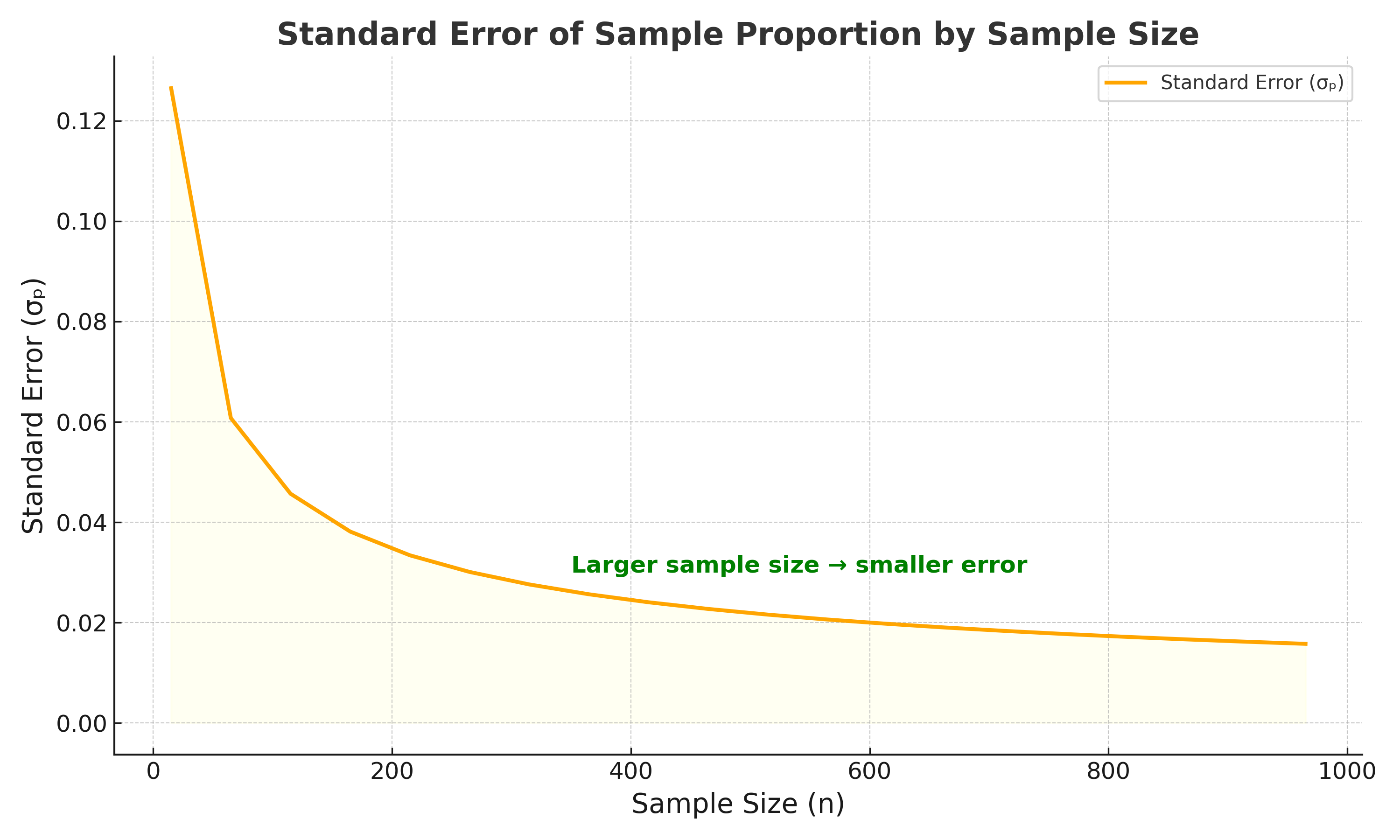
📏 Standard Deviation of the Sample Proportion

The standard deviation (also called the standard error) of the sample proportion is given by the formula:

\[ \sigma_p = \sqrt{\frac{\beta(1 - \beta)}{n}} \]

Where:

• \( \beta \) = population proportion
• \( n \) = sample size

Example:

Let’s assume a population proportion of \( \beta = 0.6 \) (60% of people support a candidate), and you take a sample of size \( n = 1000 \).

The standard error is:

\[ \sigma_p = \sqrt{\frac{0.6(1 - 0.6)}{1000}} = \sqrt{\frac{0.24}{1000}} = 0.0155 \]

This means the sample proportion will vary by about 0.0155 from the true population proportion on average.

---

⚖️ Calculating Proportions for Binary Categorical Variables

When dealing with binary categorical variables (like success/failure, yes/no), we don’t need to calculate the mean or standard deviation using traditional methods. Instead, we compute the proportion \( \beta \) for the population and \( p \) for the sample.

• Population Proportion \( \beta \)
• Sample Proportion \( p \)
• Standard Deviation of the sample proportion \( \sigma_p \)

Example:

• Population: 60% support the candidate (\( \beta = 0.6 \))
• Sample: 550 out of 1000 support the candidate (\( p = 0.55 \))

Use the formula to find the standard error for further analysis.

---

🧠 Level Up: Advanced Insights on Sampling Proportions

• The Central Limit Theorem ensures that as the sample size increases, the sampling distribution of the sample proportion becomes approximately normal, allowing for easier statistical inference.
• When sample size \( n \) is large enough (usually \( n \geq 30 \)) and both \( n\beta \geq 15 \) and \( n(1-\beta) \geq 15 \) hold, the sampling distribution of the sample proportion will follow a normal distribution.
• To improve accuracy, confidence intervals and hypothesis tests can be applied to sample proportions, leveraging the normality assumption from the CLT.
• If the sample size is small or the conditions for normality aren’t met, other techniques like binomial approximation or bootstrapping can be used for more reliable results.

---

✅ Best Practices for Proportional Sampling

• Ensure your sample size is large enough so that n × β ≥ 15 and n × (1 - β) ≥ 15.
• Use random and representative sampling to reduce bias in estimating p.
• Report a confidence interval with your sample proportion for better interpretation.
• Verify that your variable is binary (success/failure) before applying this model.

---

⚠️ Common Pitfalls to Avoid

• ❌ Applying the normal approximation when n × β or n × (1 - β) is less than 15.
• ❌ Misinterpreting p as a fixed value — it's a random variable.
• ❌ Forgetting that standard deviation decreases with larger samples.
• ❌ Confusing the population proportion β with the sample proportion p.

---

📌 Try It Yourself: Sampling Proportions

Q1: What does the sampling distribution of the sample proportion represent?

💡 Show Answer

• A) Distribution of sample proportions from many samples ✓
• B) Distribution of individual data points in the population
• C) Distribution of population proportions
• D) Distribution of standard errors

Q2: What is the central limit theorem's role in sampling distributions?

💡 Show Answer

• A) It states that the sample means follow a normal distribution, regardless of the population distribution ✓
• B) It ensures that larger sample sizes always lead to non-normal distributions
• C) It calculates the proportion of successes in the population
• D) It assumes all population distributions are normally distributed

Q3: In the formula for the standard error of the sample proportion, what does \( n \) represent?

💡 Show Answer

• A) The population size
• B) The sample size ✓
• C) The proportion of successes
• D) The standard deviation of the population

Q4: For the sampling distribution of the sample proportion to be approximately normal, which condition must hold?

💡 Show Answer

• A) \( n \times \beta \geq 15 \) and \( n \times (1 - \beta) \geq 15 \) ✓
• B) \( n \times \beta \geq 10 \) and \( n \times (1 - \beta) \geq 10 \)
• C) \( n \geq 50 \)
• D) The population proportion \( \beta \) must be 0.5

Q5: How is the standard deviation (standard error) of the sample proportion calculated?

💡 Show Answer

• A) \( \sigma_p = \frac{\beta(1 - \beta)}{n} \)
• B) \( \sigma_p = \frac{\sigma}{\sqrt{n}} \)
• C) \( \sigma_p = \sqrt{\frac{\beta(1 - \beta)}{n}} \) ✓
• D) \( \sigma_p = \frac{\beta}{n} \)

---

✅ Summary

Concept	Description
Population Proportion (\( \beta \))	Proportion of successful outcomes in the population.
Sample Proportion (\( p \))	Proportion of successful outcomes in a sample.
Sampling Distribution	Theoretical distribution of sample proportions from many samples
Mean of Sampling Distribution	Equals the population proportion \( \mu_p = \mu \)
Standard Error (\( \sigma_p \))	\( \sigma_p = \sqrt{\frac{\beta(1 - \beta)}{n}} \), variability of sample proportions
Conditions for Normality	\( n \times \beta \geq 15 \) and \( n \times (1 - \beta) \geq 15 \) for bell-shaped curve.

---

💬 Got a question or suggestion?

Leave a comment below — I’d love to hear your thoughts or help if something was unclear.

---

🔜 Up Next

In the next post, we’ll explore The Sampling Distribution of the Sample Mean in more detail — how sample averages behave and how to apply them in statistical procedures.

Stay curious! 📈