From Sample to Population: Basics of Sampling in Statistics

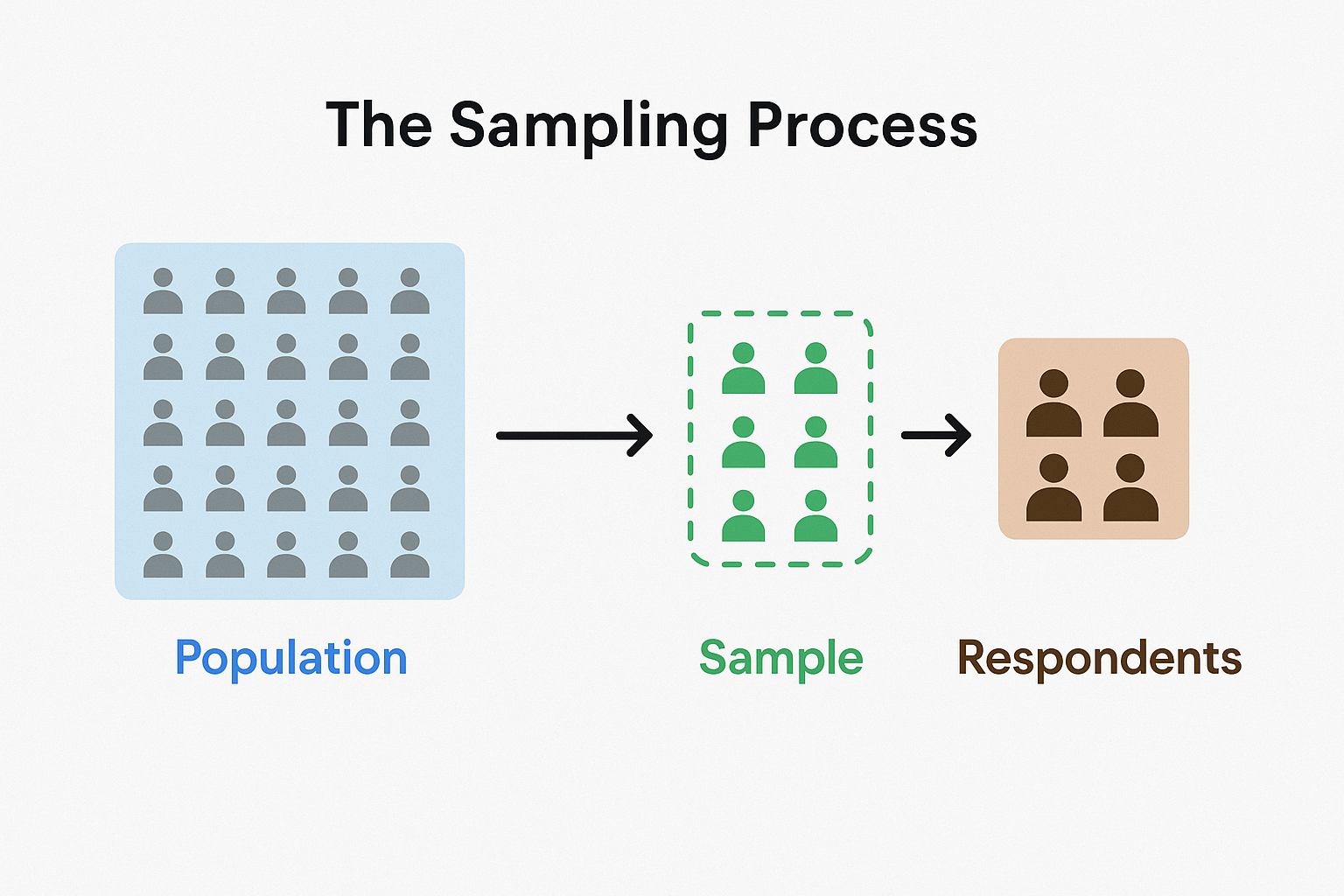
🎯 What’s the Difference Between a Population and a Sample?

Understanding the difference between a population and a sample is fundamental to mastering statistics and data analysis. A population includes every individual or observation of interest, while a sample is a representative subset used to make inferences.
Sampling lets you draw powerful conclusions without collecting data from everyone — a key principle behind both inferential statistics and machine learning.

---

📚 This post is part of the "Intro to Statistics" series

🔙 Previously: Understanding Binomial Distribution

🔜 Next: Understanding the Sampling Distribution of the Sample Mean and the Central Limit Theorem

---

🔍 Parameters vs. Statistics

When we study data:

• The characteristics of a population are called parameters — written using Greek letters (e.g., \( \mu \), \( \sigma \)).
• The characteristics of a sample are called statistics — written using Roman letters (e.g., \( \bar{x} \), \( s \)).

We use inferential statistics to predict population parameters from sample statistics.

---

🧪 The Importance of Simple Random Sampling

To make sure our sample fairly represents the population, we often use a Simple Random Sample (SRS).

In SRS:

• Every member of the population has an equal chance of being selected.
• This helps reduce bias and increases the accuracy of our predictions.

---

🧭 How to Take a Simple Random Sample

1. Define your population.
2. Create a sampling frame — a complete list of all cases.
3. Use random methods (like a random number generator) to select your sample.
4. Contact the selected respondents using:
   • Face-to-face interviews
   • Phone calls
   • Online or paper questionnaires (easiest but less accurate)

---

⚠️ Common Sampling Errors and Biases

Even with careful planning, things can go wrong:

• Undercoverage Bias: Not all classes or groups are included in the sampling frame.
• Sampling Bias: For example, choosing a convenient sample (only nearby people).
• Non-response Bias: Selected individuals don’t respond.
• Response Bias: People give inaccurate answers (on purpose or by mistake).

🎯 Making a truly random sample is not easy, especially with real-world constraints.

---

🧰 Other Sampling Techniques

When Simple Random Sampling is too difficult, we use other methods:

1. Stratified Random Sampling

• The population is divided into groups (strata).
• A random sample is taken from each stratum.
• Works best when strata are clearly defined and understood.

2. Multistage Cluster Sampling

• Useful when there is no complete sampling frame.
• Select groups (clusters) randomly, then sample within them.

✅ In both techniques, knowing the population structure (strata or clusters) is key.

---

📡 Relevance to Machine Learning

Understanding sampling is critical for:

• Model training: Most ML models are trained on a sample (training set), not the full population.
• Avoiding bias: Biased sampling can lead to models that don’t generalize well.
• Cross-validation: Techniques like k-fold cross-validation depend on fair random samples.
• Data imbalance: Knowing how to sample different classes correctly can improve classification performance.

💡 Whether you’re balancing a dataset, evaluating a model, or testing generalization — sampling is at the heart of fair ML workflows.

---

📏 Bigger Is Better… But Randomness Matters

• A larger sample reduces random error.
• But if it’s not random, the results can still be misleading.

🎯 Randomness beats size if you must choose.

---

🧠 Level Up: Real-World Sampling Challenges

• Sampling frames may be outdated or incomplete — especially in population surveys.
• People may opt out of participation, especially in phone or online surveys.
• Oversampling certain strata is a valid strategy when some groups are small but important.
• Weighting responses after collection can help adjust for biases — but requires expertise.

---

✅ Best Practices in Sampling

• Define your population clearly before sampling.
• Prefer Simple Random Sampling when feasible — it minimizes bias.
• Use stratified sampling when subgroups vary significantly.
• Keep sampling frames up to date to avoid undercoverage.

---

⚠️ Common Pitfalls

• ❌ Using convenience samples — these rarely generalize well.
• ❌ Ignoring non-response bias in surveys.
• ❌ Overgeneralizing from a small or biased sample.
• ❌ Confusing sample statistics with population parameters without inference.

---

📌 Try It Yourself: Sampling Basics

Q1: Which of the following best describes a parameter?

💡 Show Answer

✅ B) A value that describes a population
A parameter is a fixed value that summarizes some aspect of the population (like the true mean or proportion).

Q2: What is the main reason for using a sample?

💡 Show Answer

✅ A) To save cost and effort
Collecting data from an entire population is often impractical, so we sample to gain insights efficiently.

Q3: What makes Simple Random Sampling "random"?

💡 Show Answer

✅ B) Every individual has an equal chance
This ensures fairness and reduces selection bias.

Q4: Which bias happens when certain groups are not in the sampling frame?

💡 Show Answer

✅ C) Undercoverage bias
This happens when the sampling frame misses part of the population (e.g., only landline users in a mobile world).

Q5: Which sampling method works best when strata are known?

💡 Show Answer

✅ B) Stratified random sampling
Stratified sampling divides the population into known groups (strata) and samples within each group.

---

✅ Summary

Concept	Description
Population	The entire group you’re interested in
Sample	A subset selected from the population
Parameters	Characteristics of population (\( \mu, \sigma \))
Statistics	Characteristics of sample (\( \bar{x}, s \))
SRS	Simple Random Sample: equal chance selection
Bias Types	Undercoverage, Sampling, Non-response, Response
Other Techniques	Stratified, Cluster sampling

---

💬 Got a question or suggestion?

Leave a comment below — I’d love to hear your thoughts or help if something was unclear.

---

🔜 Up Next

In the next post, we’ll explore the Sampling Distribution of the Sample Mean — how sample averages behave, the Central Limit Theorem, and why these concepts form the foundation of many statistical procedures

Stay curious! 📊