Making Sense of Probabilities: Union, Tables, and Conditional Thinking
When working with data, it’s critical to understand how probabilities interact — especially when events overlap or depend on one another. In this post, you’ll learn how to calculate unions, read contingency tables, and understand conditional probabilities using intuitive visuals and real-life examples.
📚 This post is part of the "Intro to Statistics" series
🔙 Previously:How Random Is Random? Understanding Probability and Events
🔜 Next: Understanding Bayez-Rule<
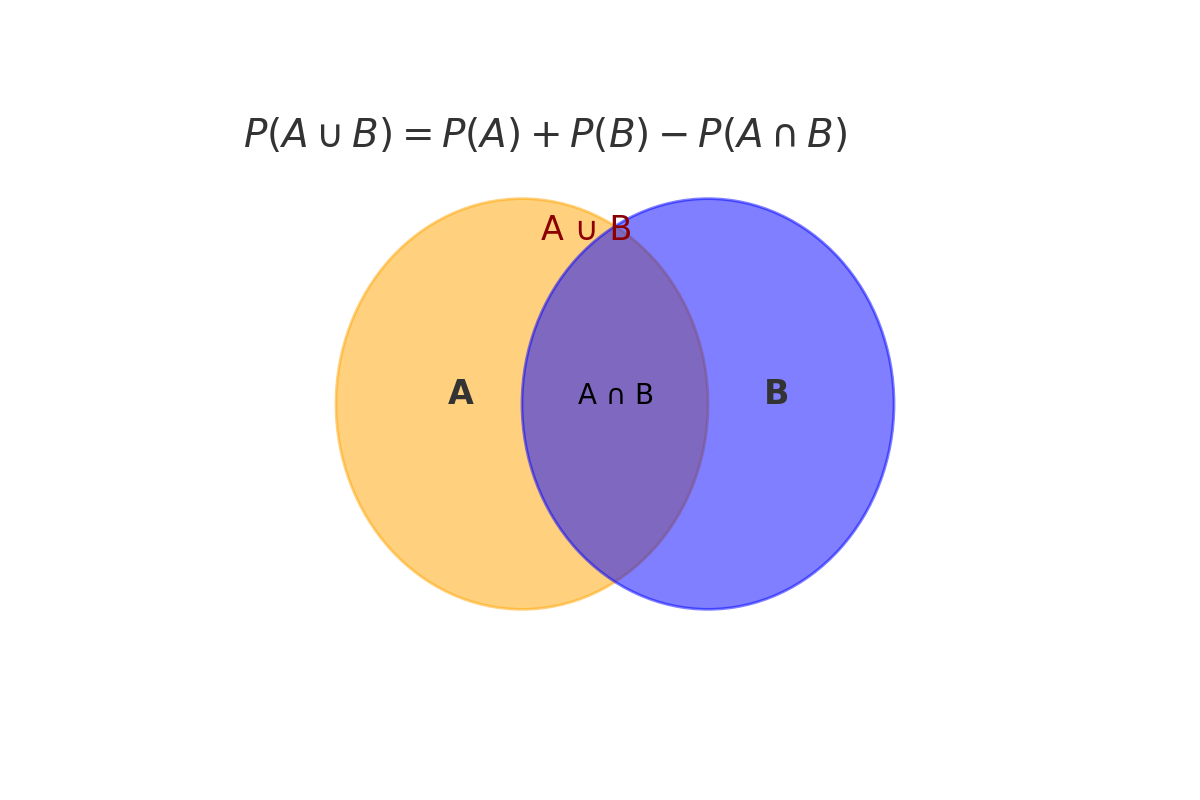
🔗 Union of Events: The Addition Rule
When calculating the probability of A or B, we combine the probabilities — but subtract any overlap:
\[ P(A \cup B) = P(A) + P(B) - P(A \cap B) \]
This is called the Addition Rule.
✅ Special Case: Disjoint Events
If A and B are mutually exclusive (disjoint), then \( P(A \cap B) = 0 \), so:
\[ P(A \cup B) = P(A) + P(B) \]
📊 Visual Aid Placeholder
📊 Marginal and Joint Proportions with Tables
Let’s say we ask 100 people whether they own a dog or a cat:
| Owns Dog | No Dog | Total | |
|---|---|---|---|
| Owns Cat | 20 | 30 | 50 |
| No Cat | 25 | 25 | 50 |
| Total | 45 | 55 | 100 |
🧩 What Are Margins?
- The totals in the last row and column are called marginal totals.
- Their proportions (divided by total) are marginal proportions:
- Example: \( P(\text{Owns Dog}) = 45 / 100 = 0.45 \)
🔄 Joint Probability Table
To convert to probabilities, divide each cell by total:
| Owns Dog (D) | No Dog | Total | |
|---|---|---|---|
| Owns Cat (C) | 0.20 | 0.30 | 0.50 |
| No Cat | 0.25 | 0.25 | 0.50 |
| Total | 0.45 | 0.55 | 1.00 |
These are joint probabilities (each cell shows \( P(C \cap D) \), etc).
✅ Total of each row/column = 1
✅ This set of events is jointly exhaustive
💡 You can compute marginal probabilities by summing across rows or columns.
⚠️ But you can’t always reverse this — joint probability can’t be recovered from marginal alone.
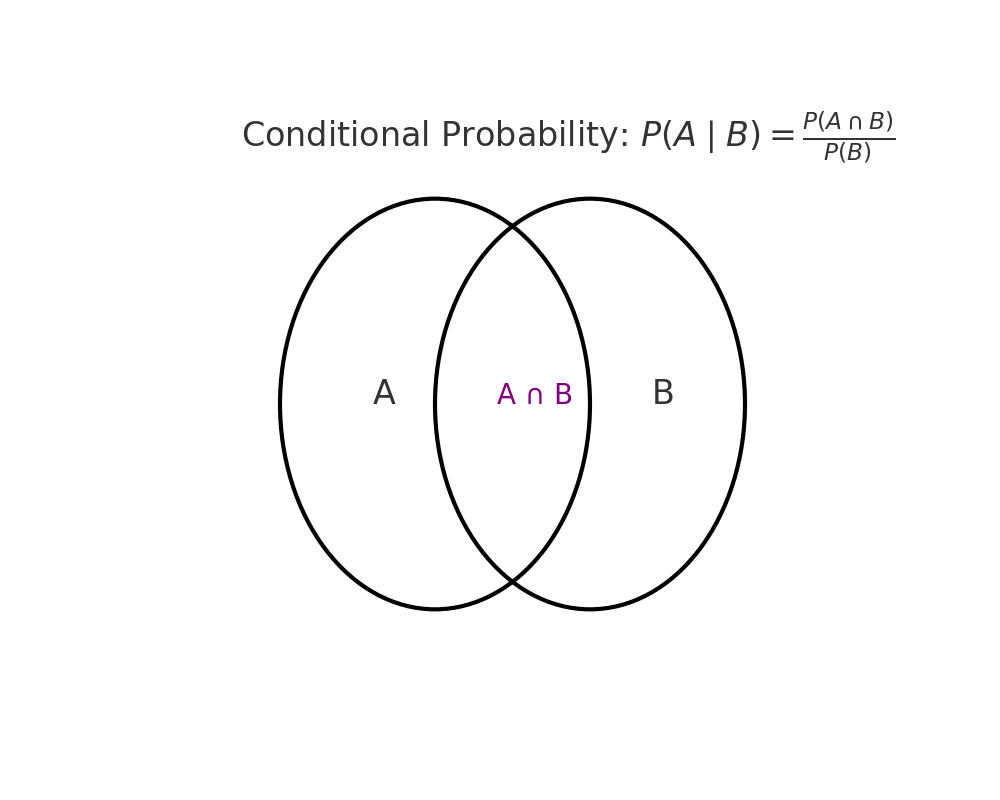
📌 Conditional Probability: What If We Know B Happened?
Conditional probability is:
\[ P(A \mid B) = \frac{P(A \cap B)}{P(B)} \]
Read as “the probability of A given B.”
📊 Venn Diagram Placeholder
🧪 Problem 1 — Using the Table
Q: What’s the probability that a person owns a cat given they own a dog?
\[ P(\text{Cat} \mid \text{Dog}) = \frac{P(\text{Cat and Dog})}{P(\text{Dog})} = \frac{0.20}{0.45} \approx 0.444 \]
🧪 Problem 2 — Medical Testing Example
| Disease (+) | No Disease (−) | Total | |
|---|---|---|---|
| Test + | 40 | 10 | 50 |
| Test − | 10 | 40 | 50 |
| Total | 50 | 50 | 100 |
Let’s convert to probabilities:
\[ P(\text{Disease} \mid \text{Test +}) = \frac{40}{50} = 0.8 \]
🧠 The test is positive, and there’s an 80% chance the person actually has the disease.
🤖 Why This Matters to Machine Learning
Understanding probability rules is foundational to many ML algorithms:
- Naive Bayes classifiers rely on conditional probability.
- Confusion matrices and precision/recall relate to joint and marginal probabilities.
- Probabilistic reasoning underlies Bayesian networks, Hidden Markov Models, and likelihood estimation.
By mastering unions, intersections, and conditional logic, you’re building the intuition needed for more complex ML reasoning.
📌 Try It Yourself: Union & Conditional Thinking
Q1: If events A and B are disjoint, what is P(A ∪ B)?
💡 Show Answer
P(A ∪ B) = P(A) + P(B) — because disjoint events can’t happen together, so there’s no overlap to subtract.
Q2: In a contingency table, how do you calculate a joint probability?
💡 Show Answer
Divide the frequency in a single cell by the total sample size. P(A ∩ B) = count in cell / grand total
Q3: What are marginal probabilities and where do you find them?
💡 Show Answer
They’re totals across rows or columns in a table, divided by the grand total.
They show the overall probability of a single variable.
Q4: What’s the formula for conditional probability?
💡 Show Answer
P(A | B) = P(A ∩ B) / P(B) — it’s the probability of A given B has occurred.
Q5: Why can’t marginal probabilities alone determine joint probabilities?
💡 Show Answer
Because they don’t show how two variables interact — they only describe each variable separately.
You need joint or conditional data to understand overlap.
Q6: You know that 90% of cat owners like coffee. What kind of probability is that?
💡 Show Answer
It’s a conditional probability: the chance of liking coffee given that someone owns a cat.
🧠 Level Up: Know When to Use Conditional Probabilities
Conditional probability isn’t just for math exams — it powers real-world decisions:
- 🩺 In medical testing, it tells us the chance a patient actually has a condition, given a positive test.
- 📈 In finance, it helps estimate risks based on market behavior.
- 🧠 In machine learning, it's the backbone of models like Naive Bayes and Bayesian networks.
Mastering it helps you move from counting events to thinking conditionally — just like algorithms do.
✅ Best Practices for Probability Thinking
- Use **Venn diagrams** or tables to clarify overlap and independence.
- Double-check whether events are **mutually exclusive** or **independent** — they’re not the same!
- Normalize tables to probabilities for clearer analysis.
- Label everything clearly: A, B, A ∩ B, A ∪ B, etc.
⚠️ Common Pitfalls
- ❌ Assuming disjoint events are independent.
- ❌ Forgetting to subtract the intersection in union calculations.
- ❌ Using marginal totals to infer conditional relationships directly.
🧠 Summary
| Concept | Meaning |
|---|---|
| Union of A and B | Add both, subtract intersection |
| Disjoint events | No overlap: \( P(A \cup B) = P(A) + P(B) \) |
| Marginal proportion | Total rows/columns ÷ total cases |
| Joint probability | Cell ÷ total |
| Conditional \( P(A \mid B) \) | Probability of A given B |
💬 Got a question or suggestion?
Leave a comment below — I’d love to hear your thoughts or help if something was unclear.
✅ Up Next
We’ll now explore probability rules in depth, including:
- Complement rules
- Bayes’ Theorem
- Advanced conditional reasoning
See you there!