🧮 Understanding Functions: The Foundation of Calculus (and Machine Learning!)

Functions are the foundation of calculus and the language of data science and machine learning. In this lesson, you’ll learn what a function is, the different types of functions, and how to avoid common mistakes when starting out.

---

📚 This post is part of the "Intro to Calculus" series

🔜 Next: Visualizing Multivariable Functions: Contour Plots, Vector-Valued Functions & Vector Fields (Beginner's Guide)

---

🎯 What is a Function

A function is a rule that assigns to each input exactly one output.
Domain: All possible inputs.
Range (or Codomain): All possible outputs.

---

A function is like a machine: you put in an input, and it produces an output.

---

📊 Types of Functions

1. 🧠Scalar-Valued Functions

A scalar-valued function outputs a single value (a scalar).

• Single Variable: $f(x) = 2x + 1$ Example: $f(4) = 2 \times 4 + 1 = 9$
• Multivariate (Multiple Inputs): $f(x, y) = x^2 + y^2$
  Example: $f(1, 2) = 1^2 + 2^2 = 5$

---

Graph of a scalar-valued function: \( f(x) = x^2 \). For every input \( x \), the output is a single value \( x^2 \).

---

Surface plot of a multivariate function: \( f(x, y) = x^2 + y^2 \). Each point \((x, y)\) has one output (height).

---

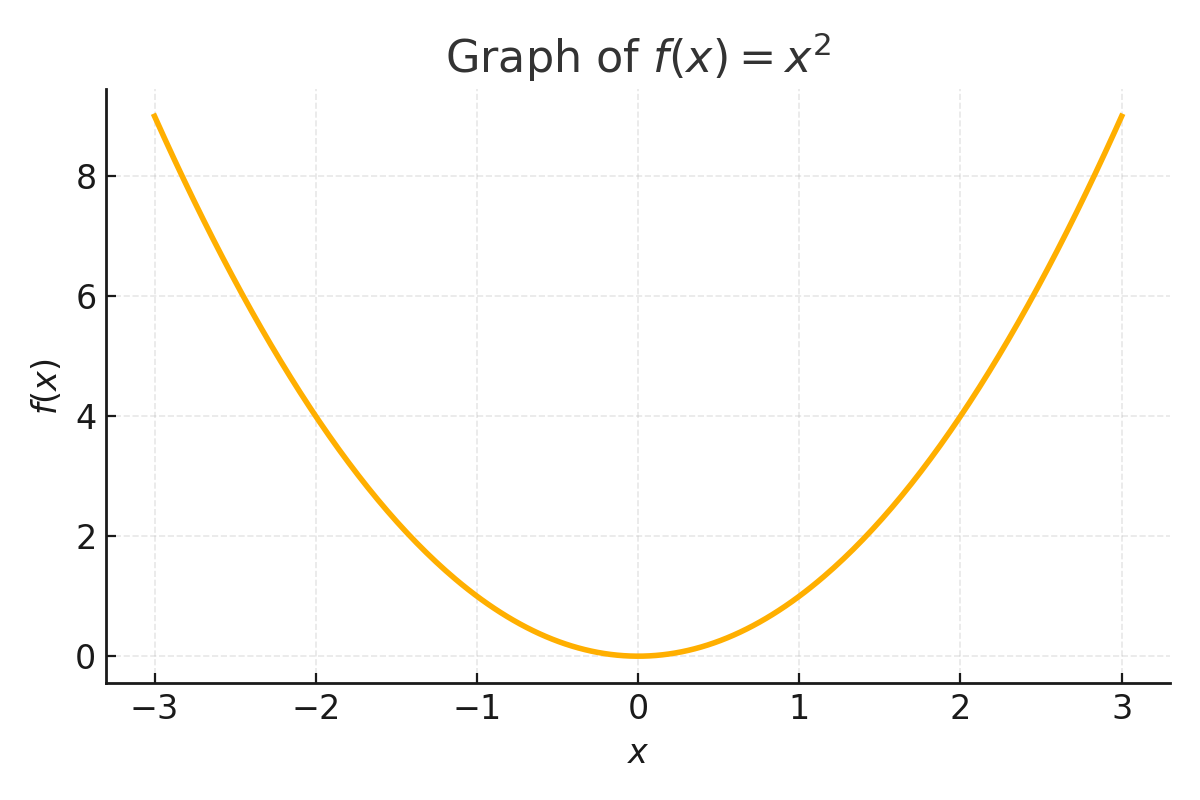
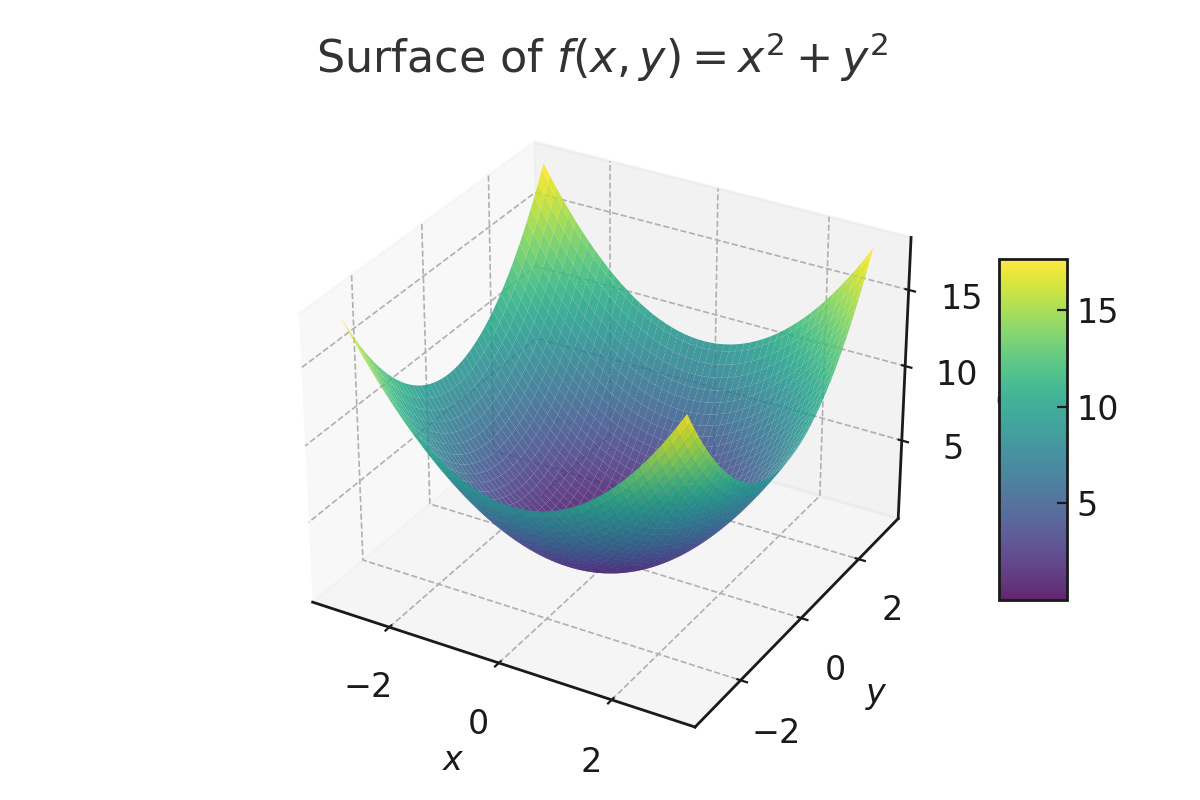
2. 📏Vector-Valued Functions

A vector-valued function outputs a vector (more than one value).

• Example: $\vec{f}(x) = (x, x^2)$
  If $x = 3$, then $\vec{f}(3) = (3, 9)$
• Multivariate Vector Function: $\vec{g}(x, y) = (x + y, x - y)$
  If $x=2, y=1$, then $\vec{g}(2,1) = (3, 1)$ —

A vector-valued function example: \( \vec{F}(x, y) = (y, -x) \). Each point has a vector as its output, visualized as arrows.

---

🔁 Real-World Example in Machine Learning:
A function can represent a model that predicts house prices:

• Input (Domain): Features (size, location, rooms, etc.)
• Output (Range): Predicted price (scalar) or probabilities (vector)

---

🤖 Real-World ML Example: Functions in Machine Learning

How are functions used in machine learning?
In machine learning, almost every model is built on the concept of a function: a rule that maps input features to output predictions.

• Linear Regression: The model is a function: $f(x) = w_1 x_1 + w_2 x_2 + ... + w_n x_n + b$ — it takes inputs (features) and returns a single output (prediction).
• Neural Networks: Each layer is a function, often taking a vector as input and producing another vector as output. Stacking these gives you a composition of functions.
• Activation Functions: Functions like ReLU, sigmoid, or tanh transform data inside neural networks, controlling nonlinearity and output range.

Key Point: When you train a model, you are finding the best function (from many possible) to map your data to accurate predictions!

---

🚀 Level Up

• Start looking at function composition: combining functions lets you build more complex models, just like stacking layers in a neural network.
• Explore inverse functions: useful for undoing operations and solving equations — important for feature scaling in ML.
• Learn to spot linear vs. non-linear functions; this distinction is key in understanding why some models are simple and others capture complex patterns.
• Check out piecewise functions: they behave differently in different input ranges (think activation functions like ReLU in deep learning).
• Get familiar with parameterized functions (like $f(x; \theta)$): these are everywhere in statistics and machine learning models.

---

✅ Best Practices

• ✅Always identify the domain (input space) and range (output space).
• ✅Work through examples by plugging in values.
• ✅Draw graphs for intuition whenever possible.
• ✅Pay attention to whether the function’s output is a scalar or a vector.
• ✅Relate the math to practical machine learning or data problems.

---

⚠️ Common Pitfalls

• ❌Forgetting to define the domain: not every input may be valid.
• ❌Mixing up input and output types (scalar vs. vector).
• ❌Not paying attention to function notation (univariate, multivariate, vector-valued).
• ❌Assuming every function is linear—many are not!

---

📌 Try It Yourself

🧩 Is \( f(x) = 2x + 3 \) a scalar-valued or vector-valued function?

It's a scalar-valued function — for any input \( x \), it produces a single number.

🧩 What is the output of the function \( f(x, y) = x^2 + y^2 \) if \( x = 1 \), \( y = 2 \)?

\[ f(1,2) = 1^2 + 2^2 = 1 + 4 = 5 \]

🧩 If \( \vec{g}(x) = (x, 2x) \), what is \( \vec{g}(3) \)?

\[ \vec{g}(3) = (3, 6) \]

🧩 True or False: A function can have two different outputs for the same input.

False. By definition, a function assigns exactly one output for each input in its domain.

---

🔁 Summary: What You Learned

Concept	Description
Function	A rule that maps each input (from the domain) to one output (in the range)
Domain	The set of all possible input values for a function
Range / Codomain	The set of all possible outputs a function can produce
Scalar-Valued Function	A function whose output is a single number (scalar)
Vector-Valued Function	A function whose output is a vector (multiple numbers)
Univariate Function	A function with a single input variable (e.g., ( f(x) ))
Multivariate Function	A function with two or more input variables (e.g., ( f(x, y) ))
Example	( f(x, y) = x^2 + y^2 ) is a multivariate, scalar-valued function

Mastering these basics will help you tackle calculus concepts like derivatives, gradients, and more advanced machine learning models in future lessons!

---

💬 Got a question or suggestion?

Leave a comment below — I’d love to hear your thoughts or help if something was unclear.

---

🧭 Next Up:

In the next post, we’ll visualize how functions behave in multiple dimensions by exploring contour plots for multivariate functions.

You’ll also get a deeper dive into vector-valued functions with clear definitions and practical examples.

Stay curious!