🔍 What is a Derivative? (Beginner’s Guide to Calculus for ML)
Before building powerful machine learning models, it’s crucial to understand the math that drives them — starting with derivatives.
In this beginner-friendly guide, you’ll learn:
- What a derivative means in simple terms
- How it’s connected to slope, gradient, and rate of change
- Why it’s essential in both calculus and machine learning
Whether you’re studying differentiation, exploring calculus basics, or diving into ML training algorithms like gradient descent, this post will give you the solid foundation you need.
Let’s break it down step-by-step with visuals, formulas, and real-world intuition.
📚 This post is part of the "Intro to Calculus" series
🔙 Previously: From Limits to Smoothness: Transformations, Limits, Continuity & Differentiability
🔜 Next: Understanding Gradients and Partial Derivatives (Multivariable Calculus for Machine Learning)
🎯 What is a Derivative?
A derivative tells us how a function changes — how fast it’s going up or down. It’s also called:
- Differentiation
- Gradient (common in machine learning)
- Slope or rate of change
In simple terms:
Derivative = how steep the curve is at a point.
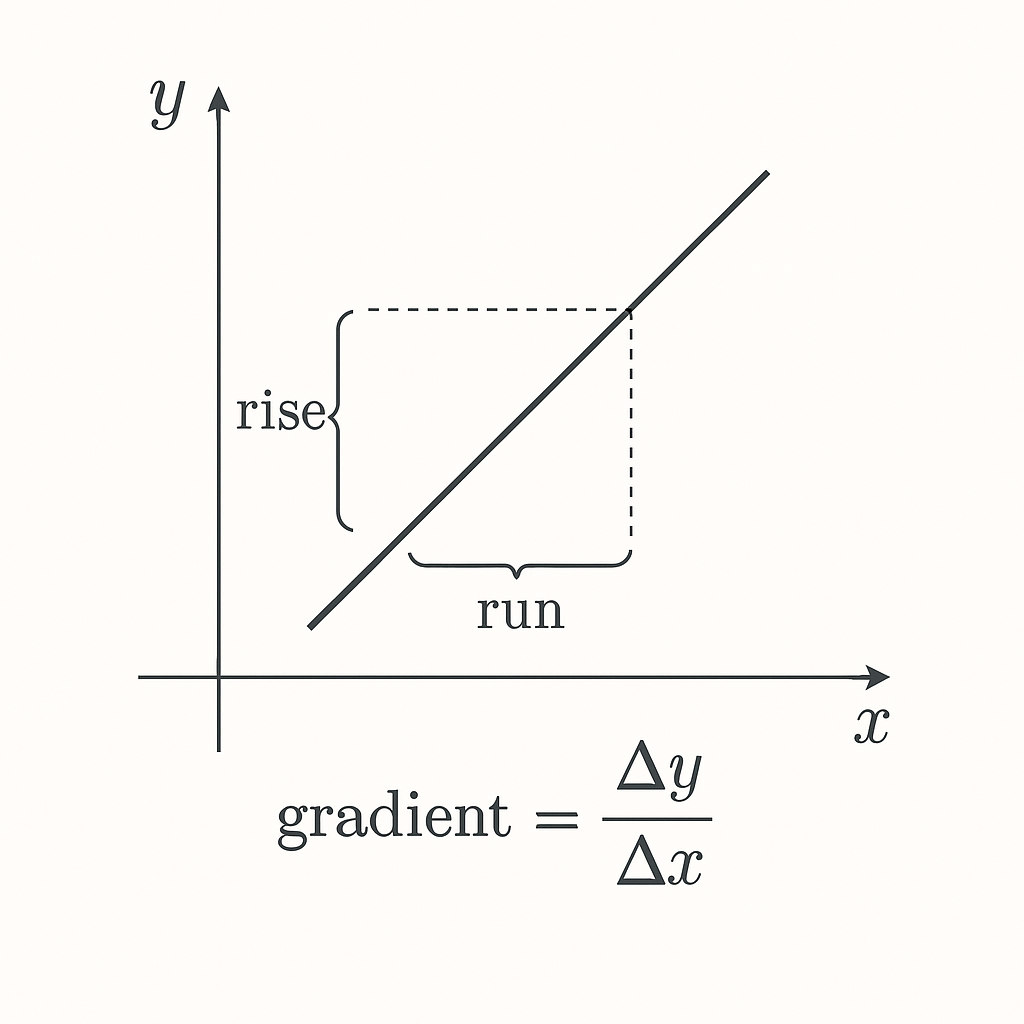
🧠 The Gradient = Rise Over Run
One of the most intuitive ways to understand this is: \[ \text{Gradient} = \frac{\Delta y}{\Delta x} \]
This is known as “rise over run” — how much the output (y) changes relative to the input (x).
📏 From Slope to Derivative
For straight lines, the slope is constant: \[ f(x) = 4x + 3 \Rightarrow \frac{d}{dx}f(x) = 4 \]
The derivative of a first-degree linear function is always constant.
Another Example:
\[ f(x) = 5x^2 \Rightarrow \frac{d}{dx}f(x) = 10x \]
In general: \[ \frac{d}{dx}(x^n) = nx^{n-1} \]
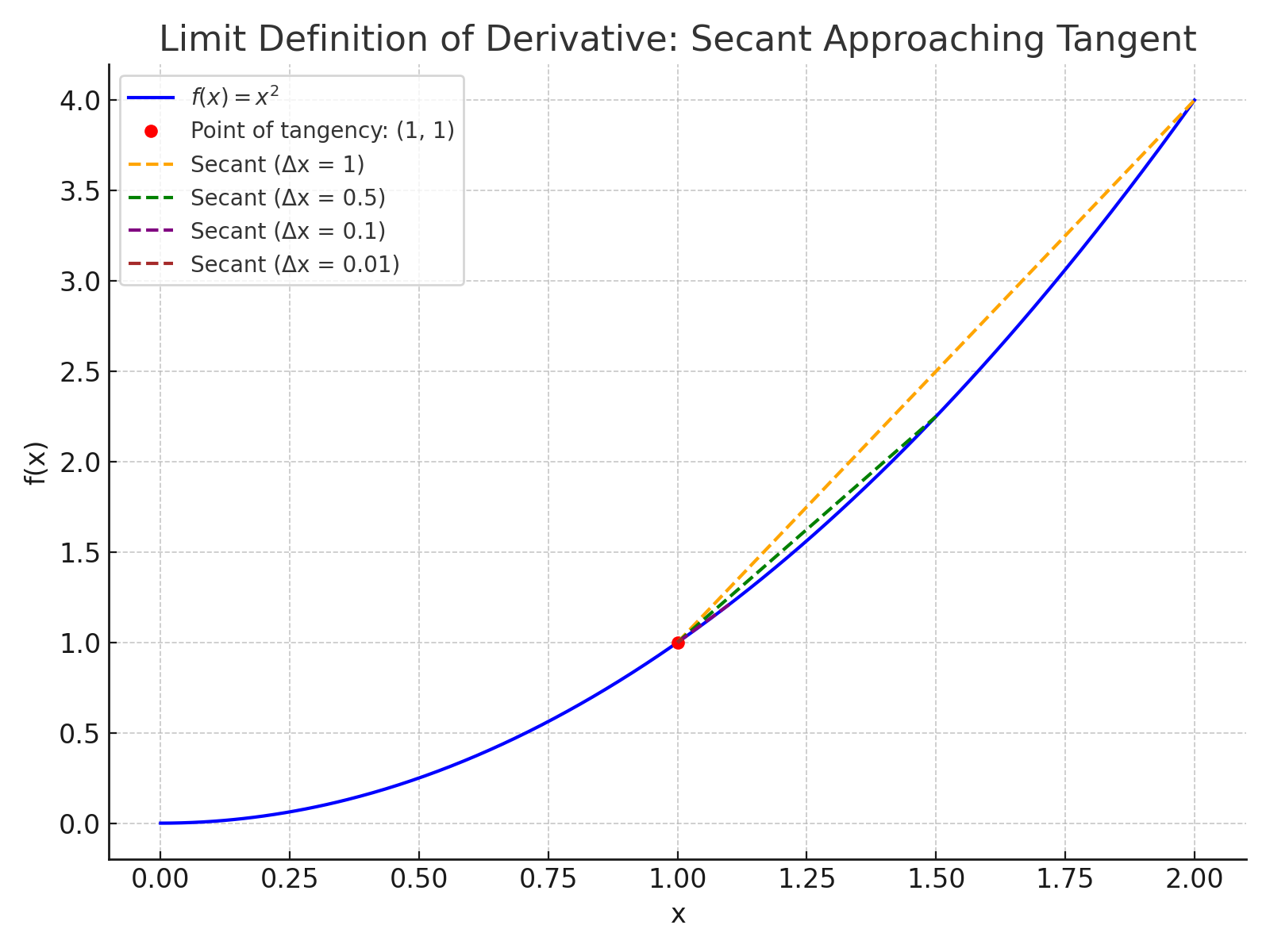
🔁 Calculus Definition (Limit Form)
To understand derivatives for curves, we define it using a limit: \[ f’(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]
This represents the instantaneous rate of change — the slope of the curve at a single point.
🔁 Example: Derivative Using the Limit Definition
Let’s use the limit form of a derivative to find the derivative of:
\[ f(x) = x^2 \]
📘 Step 1: Apply the Limit Definition
\[ f’(x) = \lim_{\Delta x \to 0} \frac{f(x + \Delta x) - f(x)}{\Delta x} \]
✍️ Step 2: Substitute the Function
\[ f(x + \Delta x) = (x + \Delta x)^2 \]
So,
\[ f’(x) = \lim_{\Delta x \to 0} \frac{(x + \Delta x)^2 - x^2}{\Delta x} \]
🧮 Step 3: Expand the Terms
\[ (x + \Delta x)^2 = x^2 + 2x\Delta x + (\Delta x)^2 \]
\[ f’(x) = \lim_{\Delta x \to 0} \frac{x^2 + 2x\Delta x + (\Delta x)^2 - x^2}{\Delta x} \]
🔄 Step 4: Simplify
Cancel out \( x^2 \):
\[ f’(x) = \lim_{\Delta x \to 0} \frac{2x\Delta x + (\Delta x)^2}{\Delta x} \]
Factor out \( \Delta x \):
\[ f’(x) = \lim_{\Delta x \to 0} \frac{\Delta x(2x + \Delta x)}{\Delta x} \]
Cancel \( \Delta x \):
\[ f’(x) = \lim_{\Delta x \to 0} (2x + \Delta x) \]
✅ Step 5: Evaluate the Limit
\[ f’(x) = 2x \]
🔚 Final Answer:
\[ \frac{d}{dx}(x^2) = 2x \]
🔢 Constant Functions
Any constant function has a flat slope: \[ \frac{d}{dx}(c) = 0 \]
For example, \( f(x) = 7 \) → derivative is 0.
🤖 Why Derivatives Matter in ML
- Gradient Descent: Optimizers rely on derivatives to minimize loss functions.
- Learning Algorithms: Many models calculate gradients to update weights.
- Curves and Features: Understanding slopes helps interpret non-linear relationships.
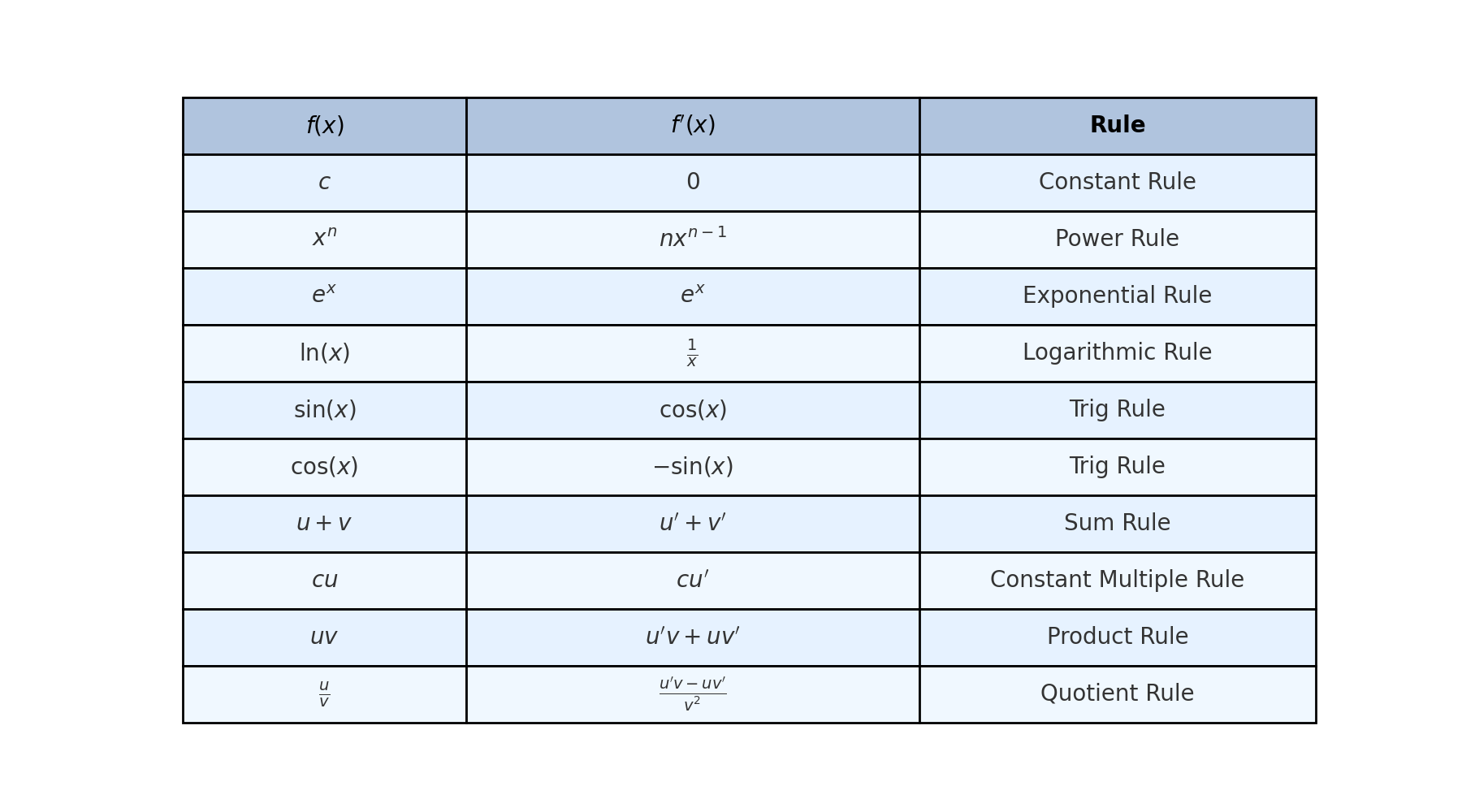
📚 Common Derivative Rules (Quick Reference)
These are the most commonly used derivatives in calculus and machine learning. Mastering them will make differentiating any function much easier.
🔹 1. Constant Rule
\[ \frac{d}{dx}(c) = 0 \] The derivative of any constant is zero.
🔹 2. Identity Rule
\[ \frac{d}{dx}(x) = 1 \] The derivative of \( x \) is just 1.
🔹 3. Constant Coefficient Rule
\[ \frac{d}{dx}(5x) = 5 \] Constants come out; you differentiate \( x \) as normal.
🔹 4. Power Rule
\[ \frac{d}{dx}(x^n) = nx^{n-1} \] For any power of \( x \), bring the power down and subtract one.
Example: \[ \frac{d}{dx}(x^5) = 5x^4 \]
🔹 5. Square Root Rule
\[ \frac{d}{dx}(\sqrt{x}) = \frac{1}{2\sqrt{x}} \]
🔹 6. Exponential Rule
\[ \frac{d}{dx}(e^x) = e^x \]
🔹 7. Logarithmic Rule
\[ \frac{d}{dx}(\ln x) = \frac{1}{x} \]
🔹 8. Product Rule
\[ \frac{d}{dx}(f \cdot g) = f \cdot \frac{d}{dx}(g) + g \cdot \frac{d}{dx}(f) \]
🔹 9. Quotient Rule
\[ \frac{d}{dx}\left(\frac{f}{g}\right) = \frac{g \cdot \frac{d}{dx}(f) - f \cdot \frac{d}{dx}(g)}{g^2} \]
🔹 10. Trigonometric Derivatives
🔸 Sine:
\[ \frac{d}{dx}(\sin x) = \cos x \]
🔸 Cosine:
\[ \frac{d}{dx}(\cos x) = -\sin x \]
🔸 Tangent:
\[ \frac{d}{dx}(\tan x) = \sec^2 x \]
🔸 Secant:
\[ \frac{d}{dx}(\sec x) = \sec x \cdot \tan x \]
🔸 Cosecant:
\[ \frac{d}{dx}(\csc x) = -\csc x \cdot \cot x \]
🔸 Cotangent:
\[ \frac{d}{dx}(\cot x) = -\csc^2 x \]
🚀 Level Up
- Derivatives are not just about slope — they’re used to find minimums and maximums in optimization problems.
- In machine learning, the concept of gradient is used in Gradient Descent, which helps models learn by adjusting weights.
- Functions with non-zero constant derivatives grow or shrink at a steady rate — just like linear trends in prediction.
- Curved functions (like \( x^2 \)) have changing slopes — understanding this helps interpret non-linear models.
- You’ll use partial derivatives when working with models that have multiple variables, like in multivariable regression or neural networks.
✅ Best Practices
- ✅ Always start with a visual — slope and tangent lines help build intuition.
- ✅ Practice on simple functions before jumping into limit-based definitions.
- ✅ Use graphing tools (e.g., Desmos, Python matplotlib) to visualize both function and derivative curves.
- ✅ Memorize and apply basic rules (like power rule and constant rule) to save time.
- ✅ Relate every new concept to how it’s used in machine learning workflows.
⚠️ Common Pitfalls
- ❌ Confusing the original function with its derivative when interpreting graphs.
- ❌ Forgetting to subtract one in the power rule (e.g., \( x^n \rightarrow nx^{n-1} \)).
- ❌ Using constant rule on variables — remember it only applies to constants.
- ❌ Ignoring the limit form when dealing with non-polynomial functions or edge cases.
- ❌ Not verifying results with graphical or numerical methods when learning.
📌 Try It Yourself
📊 What is the derivative of \( f(x) = 7x \)?
\[ f'(x) = 7 \]📊 What is the derivative of \( f(x) = 4x^3 \)?
\[ f'(x) = 12x^2 \]📊 What is the derivative of a constant function like \( f(x) = 10 \)?
\[ f'(x) = 0 \]🔁 Summary: What You Learned
| Concept | Description |
|---|---|
| Derivative | Measures how a function changes at a point |
| Gradient | Rise over run — visual slope |
| Limit Definition | Foundation of derivatives for curves |
| Power Rule | \( \frac{d}{dx}(x^n) = nx^{n-1} \) |
| Constant Rule | \( \frac{d}{dx}(c) = 0 \) |
| Linear Rule | Derivative of \( ax + b \) is \( a \) |
| From First Principles | You can derive \( f’(x) \) using the limit form |
| Example Outcome | \( \frac{d}{dx}(x^2) = 2x \) |
Understanding the basics of slope, rules, and limit-based derivatives sets the stage for more advanced tools like the Chain Rule, which we’ll cover in the next post.
💬 Got a question or suggestion?
Leave a comment below — I’d love to hear your thoughts or help if something was unclear.
🧭 Next Up:
In the next post, we’ll dive into one of the most powerful ideas in multivariable calculus — the Gradient.
You’ll learn:
- What the gradient vector means geometrically and computationally
- How to compute partial derivatives for multivariable functions
- Why the gradient shows the steepest direction of change
- How it powers optimization in machine learning (like gradient descent!)
Stay curious — the world of higher dimensions is about to open up.